H5版定点投篮游戏(1)--物理模型抽象

前言:
　　前几天目睹了大学同学开了个微店, 算是间接体验微信公众平台的使用. 觉得非常便捷和方便, 于是自己也想捣鼓一个. 公众号取名: "木目的H5游戏世界", 定位做成一个, 个人H5游戏的小站点, 同时分享游戏技术博文. 你的体验, 是对我最大的肯定.
　　本文将讲述一下定点投篮游戏的编写, 主要阐述其物理模型的抽象, 后续慢慢的完善和迭代.

构思和体验:
　　当初设想, 是做一个简单的H5游戏, 可在移动端运行. 而且入手简单, 一看即会. 但不知道做啥好? 后来看到微信朋友中有人以背身投篮照作为头像, 觉得很向上又美好. 于是想到, 是不是做个简单的定点投篮游戏呢?
　　说干就干, 因为有类似的投篮游戏App可供参考, 游戏创意不需要自己来构思, 因此算是一个模仿实现之作.
　　
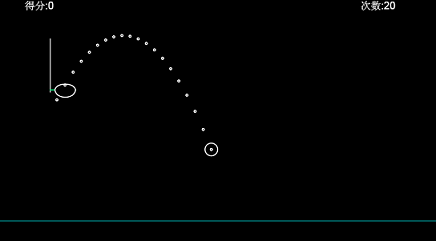
　　在线体验的游戏链接: 定点投篮游戏. (点我呀, 点我呀, ^_^!)

模型抽象:
　　游戏的主场景, 由篮板, 篮框, 篮球和地面组成. 篮球需投进篮框才能得分. 辅助线用于瞄准和定位, 简单触发即可投篮.
　　由于是2维场景, 同时涉及到简单物理碰撞和处理. 但还是决定杀鸡用牛刀------使用box2d来构建物理模型. box2d是对真实物理世界的模拟, 其谐调单位为米-千克-秒(MKS), 因此使用真实的数据去设定大小即可, 只要设定好与像素的对应缩放系数即可.
　　为了体现"专业性", 特地参考了真实篮球场的尺寸参数.
　　
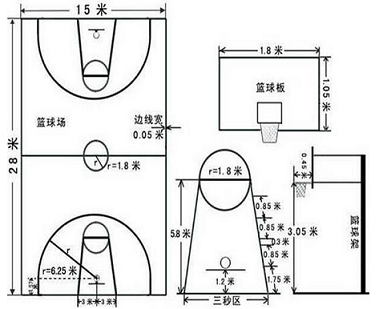
　　我们设定如下参数: 篮板高1.05米, 篮球半径为0.123米, 篮框中心半径为0.19米(比真实要小一些). 用尽量真实的数据, 在物理世界中模拟.
　　篮板是个静态刚体, 忽略其宽长, 简单设定为一条竖直的边.

// *) 创建篮板
var bodyDef = new b2BodyDef;
bodyDef.type = b2Body.b2_staticBody;

var fixDef = new b2FixtureDef;
fixDef.shape = new b2PolygonShape;
fixDef.shape.SetAsEdge(
　　new b2Vec2(1, 3),
　　new b2Vec2(1, 4.05)
);
fixDef.restitution = 1;
world.CreateBody(bodyDef).CreateFixture(fixDef);

　　篮框的设定, 所见非所得, 其用了个很trick的方法. 它的圆框在物理世界中, 并不存在, 其所拥有的就两个点: 左框点和右框点.
　　

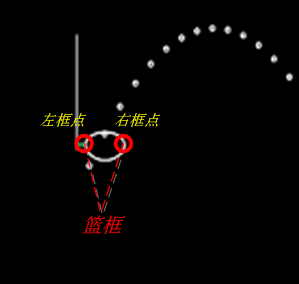
var bodyDef = new b2BodyDef;
var fixDef = new b2FixtureDef;
bodyDef.type = b2Body.b2_staticBody;

// 左框点
bodyDef.position.x = 1.09;
bodyDef.position.y = 3.05;
fixDef.shape = new b2CircleShape(0.01);
world.CreateBody(bodyDef).CreateFixture(fixDef);

// 右框点
bodyDef.position.x = 1.5;
bodyDef.position.y = 3.05;
fixDef.shape = new b2CircleShape(0.01);
world.CreateBody(bodyDef).CreateFixture(fixDef);

　　篮球是个球体, 其实动态刚体.

var bodyDef = new b2BodyDef();
bodyDef.type = b2Body.b2_dynamicBody;

var fixDef = new b2FixtureDef;
fixDef.density = 1.5;
fixDef.shape = new b2CircleShape(0.123);
world.CreateBody(bodyDef).CreateFixture(fixDef);

核心算法:
　　除了物理引擎本身的以外, 还有两个重要的核心要点. 一个是辅助抛物线, 另一个是篮球判进算法.
　　• 辅助抛物线
　　有人曾评论到, 为何"愤怒的小鸟"火极一时, 是因为人们对"抛物线"的痴迷. 因此辅助抛物线也成了这个游戏本身的核心要点. 辅助抛物线, 隐藏了投篮的角度和力量设定, 使得游戏非常容易入手. 其采用模拟描点法来进行绘制. 而不是反过来算的抛物线方程, 再来计算轨道点.

var dt = 0.62;
for (var i = 0; i < dlevel; i++) {
　　var tx = spx * dt * i + this.posx * scaleFactor;
　　var ty = spy * dt * i - 0.5 * gavity * dt * dt * i * i + this.posy * scaleFactor;
　　this.tracklines[i].drawCircle(cc.p(tx, ty), 2, cc.degreesToRadians(180), 100, false, cc.color(0, 0, 0, 255));
}

　　注: 由物理公式得: Sx = Vx * t, Sy = Vy * t + 1/2 * a * t^2; Vx, Vy由投掷点决定.
　　• 篮球判进判定算法
　　问题的本质就是如何判定篮球球心通过球框的直径线段? 这个问题, 可以稍作变换. 记录运动篮球的前后两个时间点的圆心位置, 若该两个点构成的线段, 与 蓝框直径构成的线段相交. 则认为篮球球心过了直径线段. 即进球了.
　　所以问题最终演化为, 求解两个线段相交的判断问题了?
　　
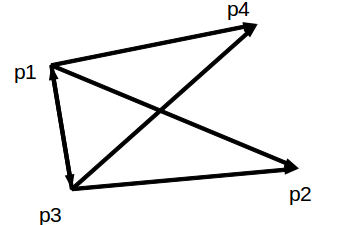
　　具体算法, 可参见如下博文: 判断两线段是否相交. 引入了快速测试和跨立试验这两个阶段.
　　这边的大致算法代码描述如下:

collideWith:function(ball) {
　　// *)
　　var px1 = ball.prevposx;
　　var py1 = ball.prevposy;
　　var px2 = ball.posx;
　　var py2 = ball.posy;

　　var qx1 = 1.1, qx2 = 1.5;
　　var qy1 = 3.05, qy2 = 3.05;

　　// *) 快速测试,
　　if (!(Math.min(px1, px2) <= Math.max(qx1, qx2)
　　　　　　&& Math.min(qx1, qx2) <= Math.max(px1, px2)
　　　　　　&& Math.min(py1, py2) <= Math.max(qy1, qy2)
　　　　　　&& Math.min(qy1, qy2) <= Math.max(py1, py2))) {
　　　　return false;
　　}

　　// *) 交叉判定
　　var d1 = (px1 - qx1) * (qy2 - qy1) - (qx2 - qx1) * (py1 - qy1);
　　var d2 = (px2 - qx1) * (qy2 - qy1) - (qx2 - qx1) * (py2 - qy1);
　　
　　var d3 = (qx1 - px1) * (py2 - py1) - (px2 - px1) * (qy1 - py1);
　　var d4 = (qx2 - px1) * (py2 - py1) - (px2 - px1) * (qy2 - py1);

　　if (d1 * d2 < 0 && d3 * d4 < 0) {
　　　　return true;
　　} else if ( d1 == 0 && this.isOnSegline(qx1, qy1, qx2, qy2, px1, py1) ) {
　　　　return true;
　　} else if ( d2 == 0 && this.isOnSegline(qx1, qy1, qx2, qy2, px2, py2) ) {
　　　　return true;
　　} else if ( d3 == 0 && this.isOnSegline(px1, py1, px2, py2, qx1, qy1) ) {
　　　　return true;
　　} else if ( d4 == 0 && this.isOnSegline(px1, py1, px2, py2, qx2, qy2) ) {
　　　　return true;
　　}
　　return false;
},
isOnSegline: function(px1, py1, px2, py2, px3,py3) {
　　var minx = Math.min(px1, px2);
　　var maxx = Math.max(px1, px2);
　　var miny = Math.min(py1, py2);
　　var maxy = Math.max(py1, py2);
　　return px3 >= minx && px3 <= maxx && py3 >= miny && py3 <= maxy;
}

总结:
　　朋友玩了一把, 吐槽不少, 不过还是很开心, 能体验就是种肯定. 后期一定好好再改善一把, 使得其用户体验上, 更加友好.

写在最后：
　　如果你觉得这篇文章对你有帮助, 请小小打赏下. 其实我想试试, 看看写博客能否给自己带来一点小小的收益. 无论多少, 都是对楼主一种由衷的肯定.

　　

公众号&游戏站点:
　　个人微信公众号: 木目的H5游戏世界