HDU 4947 GCD Array 容斥原理+树状数组

GCD Array

Time Limit: 11000/5500 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 843    Accepted Submission(s):
205

Problem Description

Teacher Mai finds that many problems about arithmetic
function can be reduced to the following problem:

Maintain an array a
with index from 1 to l. There are two kinds of operations:

1. Add v to
a_x for every x that gcd(x,n)=d.
  2. Query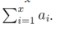

 

Input

There are multiple test cases, terminated by a line "0
0".

For each test case, the first line contains two integers
l,Q(1<=l,Q<=5*10^4), indicating the length of the array and the number of
the operations.

In following Q lines, each line indicates an operation,
and the format is "1 n d v" or "2 x"
(1<=n,d,v<=2*10^5,1<=x<=l).

 

Output

For each case, output "Case #k:" first, where k is the
case number counting from 1.

Then output the answer to each query.

 

Sample Input

6 4

1 4 1 2

2 5

1 3 3 3

2 3

0 0

 

Sample Output

 

Case #1:

6

7

 

Author

xudyh

 

Source

2014
Multi-University Training Contest 8

 

 题意：2个操作

         在长度长度为len的数组操作

         1 n v d 给数组x下标满足 gcd(x,n)=d的对应位置+v.

         2 x 询问数组sum(a1,,,ax)的和

思路：如果一个一个更新是会超时的。

        方法大致是这样，首先和GCD（）问题类似，从反面着手，首先全部数字+v，然后在gcd（x,n)!=d的位置-v。

        gcd（x,n) = d 可以转化为gcd(x/d,n/d)=1; 转化为求互质。这个应该容易理解些。

        现在我设立一个数组a[ ] ,a[i] 代表的意思是 gcd（x,n)为i的倍数的时候的方案数。

　　  那么原来的问题，N = n/d ，现在就分解N的素因子，并进行容斥。比如6 ： 2 ， 3 ， -6.

        首先在所有的数字上加v，然后用容斥的结果在数组上进行对不互质的地方进行-v。

        举一个例子。

　　  比如len = 10 ， gcd（x,6) = 2; ==> gcd(x/2,3)=1;

       那么我们只能在[1-10/2]进行更新。

       求得的容斥结果为 2 ， 3， -6.那么首先我们在所有的数字上+v，就是a[d]=v,(a[2]=v);

       然后在2*d上减去v，3*d上减去v，6*d上加上v。就是这样。

       至于为什么要*d，这个思考一下就会知道的。

       这就是第一个操作了。

       第二个操作就是询问数组【1-x】的和，转化为求数组在a[i]有多少个 x/i 个。

       就是sum(a[i]*x/i) ;由于 x/i 我们能用sqrt（）的算法来做。这里也就牵涉到求和，用树状数组。

       代码比较挫，几乎是压线过。

      

 #include<iostream>
 #include<stdio.h>
 #include<cstring>
 #include<cstdlib>
 using namespace std;
 typedef __int64 LL;

 const int maxn = +;
 const int INF = 2e5+;
 LL p[maxn];
 bool s[INF];
 int prime[],len;

 void Init()
 {
     len = ;
     memset(s,false,sizeof(s));
     for(int i=;i<INF;i++)
     {
         if(s[i]==true)continue;
         prime[++len] = i;
         for(int j=i+i;j<INF;j=j+i)
         s[j]=true;
     }
 }
 void add(int x,int n,int num1)
 {
     for(int i=x;i<=n;i=i+(i&(-i)))
     p[i] = p[i] + num1;
 }
 LL query(int x)
 {
     if(x==)return ;
     LL sum1 = ;
     while(x)
     {
         sum1=sum1+p[x];
         x=x-(x&(-x));
     }
     return sum1;
 }
 int Q[],yz[],ylen,qlen;
 void init(int n)
 {
     ylen = qlen = ;
     for(int i=;prime[i]*prime[i]<=n;i++)
     {
         if(n%prime[i]==)
         {
             while(n%prime[i]==) n=n/prime[i];
             yz[++ylen] = prime[i];
         }
     }
     if(n!=) yz[++ylen] = n;
     Q[]=-;
     for(int i=;i<=ylen;i++)
     {
         int k = qlen;
         for(int j=;j<=k;j++)
         Q[++qlen] = -*Q[j]*yz[i];
     }
 }
 int main()
 {
     int n,m,hxl,d,v,size1,x,T=;
     Init();
     while(scanf("%d%d",&n,&m)>)
     {
         if(n==&&m==)break;
         memset(p,,sizeof(p));
         printf("Case #%d:\n",++T);
         while(m--)
         {
             scanf("%d",&size1);
             if(size1==)
             {
                 scanf("%d%d%d",&hxl,&d,&v);
                 if(hxl%d!=)continue;
                 hxl = hxl /d;
                 int tom = n/d;
                 add(d,n,v);
                 init(hxl);
                 for(int i=;i<=qlen;i++)
                 if(Q[i]<) {
                     Q[i] = -Q[i];
                     if(Q[i]>tom)continue;
                     add(Q[i]*d,n,v);
                     }
                 else {
                     if(Q[i]>tom)continue;
                     add(Q[i]*d,n,-v);
                 }
             }
             else{
                 scanf("%d",&x);
                 LL sum1 = ;
                 for(int i=,la=;i<=x;i=la+){
                     la = x/(x/i);
                     sum1 = sum1 + (query(la)-query(i-))*(x/i);
                 }
                 printf("%I64d\n",sum1);
             }
         }
     }
     return ;
 }