【HDU4307】Matrix

本篇博客基本全篇转自https://www.cnblogs.com/staginner/archive/2012/08/13/2636826.html，太强啦ORZ

题意

A是个1*n的矩阵，每个元素是1或者0，你需要构造一个矩阵A，使得D=（A*B-C)*AT最大，其中B是个给出的n*n的矩阵，C是个给出的1*n的矩阵，他们的元素都是非负的。输出最大的D。

分析

从本质上讲，之所以能够用最大流解决这个问题，关键在于最大流可以求解下面这个函数的最小值：

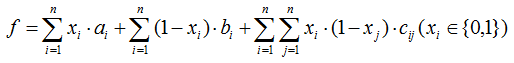
接下来就分析一下如何用最大流求解上面这个函数的极值。

首先xi一共只有两种选择，那么最终可以按xi的取值将xi划分成两个集合，那么如果xi在值为1的集合里，xj在值为0的集合里，那么就会产生一个代价cij。同时如果xi选择0就会产生一个bi的代价，如果xi选择1就会产生一个ai的代价。

于是构造一个源点S，汇点T做最小割，不妨假设做完最小割之后值为1的xi的集合是和S相连的部分，值为0的xi的集合是和T相连的部分。

由于表达式中有三项，我们用三种割边来分别描述这三项的值。一种是xi选择了1，这样就不能选择0，需要把xi-T这条边割掉，由于xi选择1会产生ai的代价，那么就把这条边的容量设为ai。另一种是xi选择了0，这样就不能选择1，需要把S-xi这条边割掉，由于xi选择0会产生bi的代价，那么就把这条边的容量设为bi。最后一种是xi选择了1，xj选择了0，这样xi和xj不能在同一个集合中，需要把xi-xj这条边割掉，由于xi选择1，xj选择0产生cij的代价，那么就把这条边的容量设为cij。

这样对建好的图做最小割就可以得到上面哪个函数的最小值。

-----------------------------------------------------------------------我是分割线--------------------------------------------------------------------------------------------------

然后我们回归原题，想办法朝上面的式子方向进行转化。

本题的计算写出来是这个样子的

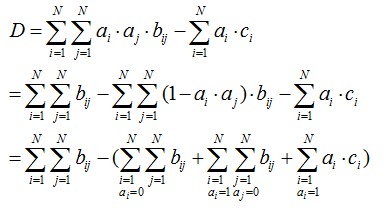
然后就可以按照上面的方法通过网络流来求解这个题。