Splay树分析

简述

　　Splay树是一种二叉查找平衡树，其又名伸展树，缘由是对其进行任意操作，树的内部结构都会发生类似伸张的动作，换言之，其读和写操作都会修改树的结构。Splay树拥有和其它二叉查找平衡树一致的读写时间复杂度O(log2(n))。Splay树的优点是实现简单（苦于红黑树的小伙伴有福了），并且功能异常强大。其缺点其一是所有操作都会修改树结构，因此对其进行的任意操作都需要进行同步，当然单线程就无需进行担心。其二是Splay树的时间复杂度的常数较大。

Splay实现

splay操作

　　Splay树的结点之间的关系与一般二叉树相同，其任意结点左孩子的关键字不会超过当前结点，其右孩子的关键字不会小于当前结点，因此按中序遍历得到的结点序列的关键字是递增的。Splay树的核心操作是splay(x)，其将结点x通过旋转移动到树的顶端。一般二叉树的旋转大家估计都见过 ，但是splay的旋转略有不同，其是通过双旋使x的深度不断降低，下面给出splay旋转的规则（总共三个）：

　　1.若x的父亲y是根结点。若x是y的左孩子，则进行下面的zig旋转（若x是y的右孩子，则进行镜像操作zag，即将所有左变为右，右变为左）

　　

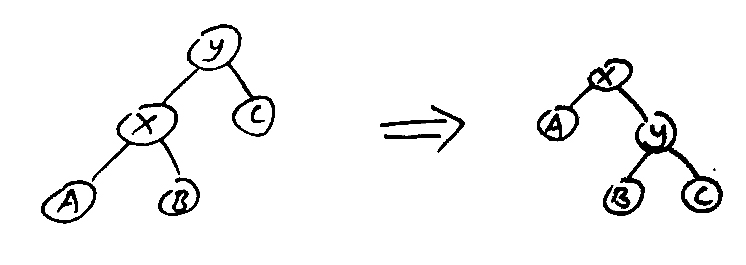
　　2.若x的父亲y不是根结点，记z为y的父亲。若x是y的左结点且y是z的左孩子，则进行下面的zigzig操作（若对称的x是y的右孩子且y是z的右孩子，则进行镜像操作zagzag）。

　　

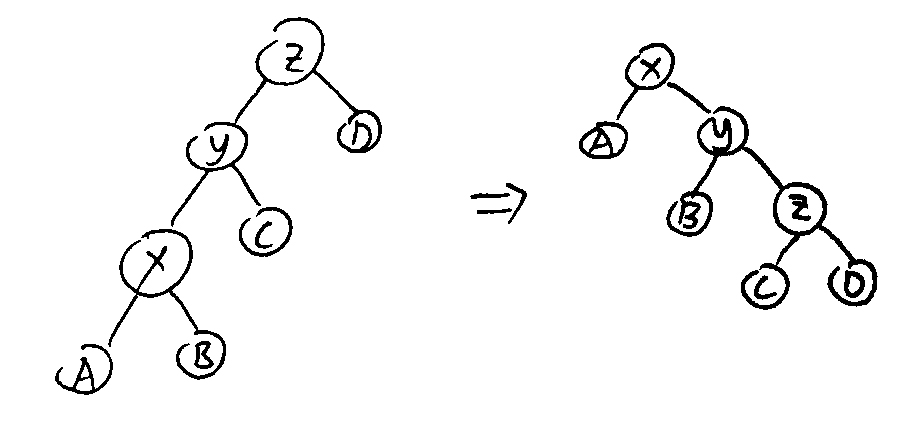
　　3.若x的父亲y不是根结点，记z为y的父亲。若x是y的右结点且y是z的左结点，则进行下面的zagzig操作（若对称的x是y的左孩子，y是z的右孩子，则进行镜像操作zigzag）。

　　我们在splay的过程中不断探测x此时的状况，并选择调用zig,zag,zigzig,zagzag,zigzag,zagzig六种操作中的一种，通过旋转使得x不断上升（x的深度降低），直到x成为树根。

　　实际上我们不需要完全为splay实现6种旋转方案，只需要实现zig和zag即可。zigzag(x)与先后调用zig(x)，zag(x)的结果一致，而zagzig则与先后调用zag(x)，zig(x)的结果一致。但是要小心zigzig(x)，其结果与调用两次zig(x)是不同的，应该是先调用zig(x.f)后调用zig(x)，这里x.f表示x的父亲，而zazag也类似，等价于先调用zag(x.f)，再调用zag(x)。这部分的说明请自行验证。

　　splay操作并不会影响对原树和新树进行中序遍历得到的结果，即对于一对原树中结点x，y，若x处于y的左子树中，则在新树中或者x处于y的左子树中，或者y处于x的右子树中。这都是来源于旋转的直接性质。

插入

　　下面说明插入insert(k)的具体流程，要插入关键字k，我们首先需要找到合适的插入位置，之后新建结点x并插入，之后对结点x进行splay操作。

连接

　　连接join(x,y)用于将以x为根和以y为根的两株splay树连接为一株树，其中x树中所有结点的关键字都不大于y树中的所有结点的关键字。如果x或y为空树，则返回另外一株树即可。否则在y中查找关键字最小的结点s，并对其调用splay操作。之后将x树作为s的左孩子进行连接。

分裂

　　split(k)，将树分裂为两株子树x与y，其中x中所有结点的关键字均小于k，而y中所有结点的关键字均大于等于k。我们先向树中插入一个关键字为k的结点x（但是插入过程中我们需要保证若某个树中结点的关键字为k，则x一定插入到该结点的左子树中），之后对x进行splay手续。此时树根为x，x的左孩子为小于k的树，右孩子则为其余结点组合成的树，移除x并返回其左右子树。

删除

　　删除操作delete(k)，删除关键字为k的任意一个结点。我们先找到某个关键字为k的结点x，若不存在，则对访问到的最深的结点f执行splay手续。否则对x执行splay操作。之后我们移除x，并将其左右子树作为两株新树，并利用连接操作进行连接。

查找

　　find(k)，查找关键字为k的任意一个结点。由于Splay树的存储是有序的，因此不断地根据子树根结点的关键字与k的关系，选择继续搜索其左子树还是右子树，或者根结点的关键字为k，这个流程与在一般二叉查找树中寻找指定关键字的步骤和流程完全相同。如果找到，则返回该结点，否则返回空。不管是否找到，在离开前，都不要忘了为查找过的最深的顶点f执行splay手续。

时间复杂度

　　很容易发现每次操作的时间复杂度与该次操作执行的splay操作的时间复杂度+O(1)是一致的，其中+O(1)是由于存在常数时间的费用。

　　我们记第i次操作前数据结构的势能为D_i-1，而第i次操作后数据结构的势能为D_i，之后定义s(x)表示以x为根结点的子树中结点总数，记d(x)=log2(s(x))，同样定义s(T)为树T中的结点总数。而我们将Splay树的势能定义为D=∑d(x)，其中x取树中的所有不同结点。记c_i表示Splay操作中第i次上升x所付出的实际时间费用，我们认为每次操作的时间费用c_i为1，即将其作为单位费用，记c_i+D_i-D_i-1为第i次上升的摊还费用。很显然D₀=0，这也是势能的下界，因此我们可以保证∑(c_i+D_i-D_i-1)=∑c_i+D_n-D₀是该次操作时间复杂度的一个上界。

　　对于一次对x的上升，其可能对应六种模式，zig，zag，zigzig，zagzag，zigzag，zagzig。不考虑镜像模式（镜像模式只是修改了左右，因此时间复杂度与原来的模式一致），我们需要分析zig，zigzig，zigzag的摊还费用。

　　对于zig操作，观察对应的图，我们可以得出下面公式的成立（结点名称后面加'表示变换后的结点）：

$$ d\left(x'\right)+d\left(y'\right)-d\left(x\right)-d\left(y\right)=d\left(y'\right)-d\left(x\right)\le d\left(x'\right)-d\left(x\right)\le 3d\left(x'\right)-3d\left(x\right) $$

　　而对于zigzig操作，观察对应的图，得出：

$$ d\left(x'\right)+d\left(y'\right)+d\left(z'\right)-d\left(x\right)-d\left(y\right)-d\left(z\right)=d\left(y'\right)+d\left(z'\right)-d\left(x\right)-d\left(y\right) $$

且由于

$$ 2d\left(x'\right)-d\left(z'\right)-d\left(x\right)=\log_2\left(\frac{\left[s\left(x'\right)\right]^2}{s\left(z'\right)s\left(x\right)}\right)\geqslant\log_2\left(4\right)=2 $$

从而得到

$$ d\left(y'\right)+d\left(z'\right)-d\left(x\right)-d\left(y\right)\le d\left(x'\right)+d\left(z'\right)-2d\left(x\right) $$ $$ \le d\left(x'\right)+d\left(z'\right)-2d\left(x\right)+2d\left(x'\right)-d\left(z'\right)-d\left(x\right)-2=3d\left(x'\right)-3d\left(x\right)-2 $$

　　再考虑zigzag操作，观察对应的图，得出：

$$ d\left(x'\right)+d\left(y'\right)+d\left(z'\right)-d\left(x\right)-d\left(y\right)-d\left(z\right)=d\left(y'\right)+d\left(z'\right)-d\left(x\right)-d\left(y\right) $$

且同样的有

$$ 2d\left(x'\right)-d\left(y'\right)-d\left(z'\right)\geqslant 2 $$

从而得到

$$ d\left(y'\right)+d\left(z'\right)-d\left(x\right)-d\left(y\right)\le d\left(y'\right)+d\left(z'\right)-2d\left(x\right) $$ $$ \le d\left(y'\right)+d\left(z'\right)-2d\left(x\right)+2d\left(x'\right)-d\left(y'\right)-d\left(z'\right)-2 $$ $$ =2d\left(x'\right)-2d\left(x\right)-2\le 3d\left(x'\right)-3d\left(x\right)-2 $$

　　可以得出zig的摊还费用上界为3d(x')-3d(x)+1，而zigzig和zigzag的摊还费用上界为3d(x')-3d(x)。由此我们可以计算出一次splay操作的摊还时间复杂度上界为（我们将开始时的x记为x₀，而第i次上升后的x记为x_i，设t为总共上升次数）：

$$ \sum_{i=1}^t{\left(3d\left(x_i\right)-3d\left(x_{i-1}\right)\right)}+O\left(1\right)+1=3d\left(T\right)-3d\left(x_0\right)+O\left(1\right)\le 3d\left(T\right)+O\left(1\right)=O\left(\log_2\left(|T|\right)\right) $$

因此我们到此已经证明了splay操作的摊还时间复杂度上界O(log2(|T|))，也间接地证明了所有splay操作的摊还时间复杂度上界均为O(log2(|T|))。