P2168 [NOI2015]荷马史诗

题目描述

追逐影子的人，自己就是影子 ——荷马

Allison 最近迷上了文学。她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了，Allison 想通过一种编码方式使得它变得短一些。

一部《荷马史诗》中有n种不同的单词，从1到n进行编号。其中第i种单词出现的总次数为wi。Allison 想要用k进制串si来替换第i种单词，使得其满足如下要求：

对于任意的 1 ≤ i, j ≤ n ， i ≠ j ，都有：si不是sj的前缀。

现在 Allison 想要知道，如何选择si，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，Allison 还想知道最长的si的最短长度是多少？

一个字符串被称为k进制字符串，当且仅当它的每个字符是 0 到 k − 1 之间（包括 0 和 k − 1 ）的整数。

字符串 str1 被称为字符串 str2 的前缀，当且仅当：存在 1 ≤ t ≤ m ，使得str1 = str2[1..t]。其中，m是字符串str2的长度，str2[1..t] 表示str2的前t个字符组成的字符串。

输入输出格式

输入格式：

输入的第 1 行包含 2 个正整数 n, k ，中间用单个空格隔开，表示共有 n种单词，需要使用k进制字符串进行替换。

接下来n行，第 i + 1 行包含 1 个非负整数wi ，表示第 i 种单词的出现次数。

输出格式：

输出包括 2 行。

第 1 行输出 1 个整数，为《荷马史诗》经过重新编码以后的最短长度。

第 2 行输出 1 个整数，为保证最短总长度的情况下，最长字符串 si 的最短长度。

输入输出样例

输入样例#1：

输出样例#1：

12

2

输入样例#2：

输出样例#2：

36

3

说明

【样例说明 1】

用 X(k) 表示 X 是以 k 进制表示的字符串。

一种最优方案：令 00(2) 替换第 1 种单词， 01(2) 替换第 2 种单词， 10(2) 替换第 3 种单词，11(2) 替换第 4 种单词。在这种方案下，编码以后的最短长度为：

1 × 2 + 1 × 2 + 2 × 2 + 2 × 2 = 12

最长字符串si的长度为 2 。

一种非最优方案：令 000(2) 替换第 1 种单词，001(2) 替换第 2 种单词，01(2)替换第 3 种单词，1(2) 替换第 4 种单词。在这种方案下，编码以后的最短长度为：

1 × 3 + 1 × 3 + 2 × 2 + 2 × 1 = 12

最长字符串 si 的长度为 3 。与最优方案相比，文章的长度相同，但是最长字符串的长度更长一些。

【样例说明 2】

一种最优方案：令 000(3) 替换第 1 种单词，001(3) 替换第 2 种单词，01(3) 替换第 3 种单词， 02(3) 替换第 4 种单词， 1(3) 替换第 5 种单词， 2(3) 替换第 6 种单词。

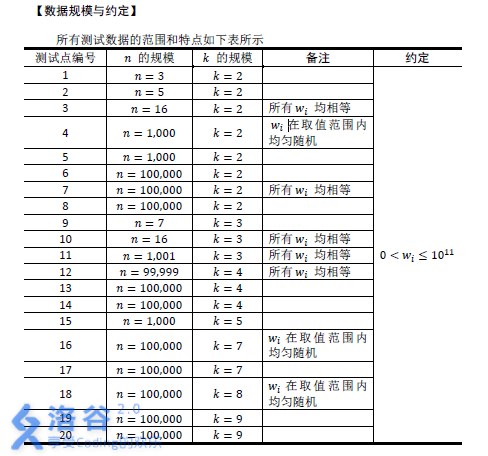
【提示】

选手请注意使用 64 位整数进行输入输出、存储和计算。

Solution:

　　本题哈夫曼树裸题。

　　给定一个$k$叉树，每个单词的出现次数$w_1,w_2…w_n$为$n$个叶子节点的权值，最后合并成一个节点就等价于把所有叶子节点替换掉。而题意中的用$k$进制串去替换，我们可以将每个节点的$k$个分叉由$0\rightarrow k-1$编号，那么根节点到某一叶子节点的路径所表示的$k$进制串就是替换掉该叶子节点的串，且它对于答案的贡献（串的长度）恰好就是该叶子节点合并的次数。然后题目中的限制条件$s_i$不为$s_j$的前缀，其实只要把整棵哈夫曼树看作一个$Trie$树，那么就不难发现$s_i$的前缀的末节点一定为根节点到某一叶节点的路径所经过的内部节点，而我们实现哈夫曼树时，一个串的末节点肯定是树的叶子节点，所以该性质一定能满足。至于求最长的$s_i$最短，其实就是使得树的最大深度最小（叶子节点合并次数最大值最小），不难想到一个贪心，就是当出现多个$w_i$相同时，优先合并深度小的，这样就能解决该问题。

代码：

#include<bits/stdc++.h>

#define il inline

#define ll long long

#define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)

#define Bor(i,a,b) for(int (i)=(b);(i)>=(a);(i)--)

using namespace std;

ll n,k,ans,minn;

struct node{

    ll w,d;

    node(ll a,ll b){w=a;d=b;}

    bool operator<(const node &a)const {return w==a.w?d>a.d:w>a.w;}

};

priority_queue<node>q;

il ll gi(){

    ll a=;char x=getchar();bool f=;

    while((x<''||x>'')&&x!='-')x=getchar();

    if(x=='-')x=getchar(),f=;

    while(x>=''&&x<='')a=(a<<)+(a<<)+x-,x=getchar();

    return f?-a:a;

}

int main(){

    n=gi(),k=gi();

    ll p=(n-)%(k-),tot;

    if(p) p=k--p;

    ll m=n+p;

    while(p--) q.push(node(,));

    while(n--) p=gi(),q.push(node(p,));

    while(!q.empty()){

        if(m==)break;

        tot=,p=;

        For(i,,k) tot+=q.top().w,p=max(p,q.top().d),q.pop();

        q.push(node(tot,p+));ans+=tot;

        m-=(k-);

    }

    cout<<ans<<endl<<q.top().d;

    return ;

}