后向传播算法“backpropragation”详解

为什么要使用backpropagation?

梯度下降不用多说，如果不清楚的可以参考梯度下降算法。

神经网络的参数集合theta，包括超级多组weight和bais。

要使用梯度下降，就需要计算每一个参数的梯度，但是神经网络常常有数以万计，甚至百万的参数，所以需要使用backpropagation来高效地计算梯度。

backpropagation的推导

backpropagation背后的原理其实很简单，就是求导的链式法则。

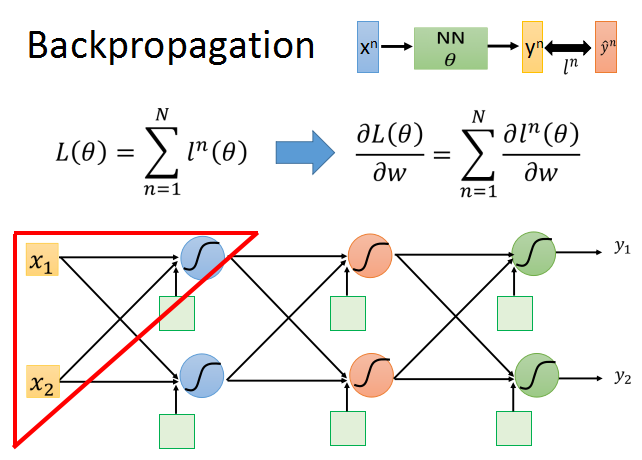
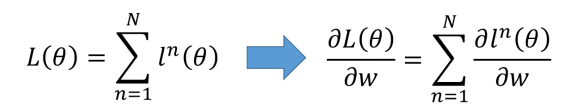
我们从上面的公式开始推导。以其中一个神经元为例。

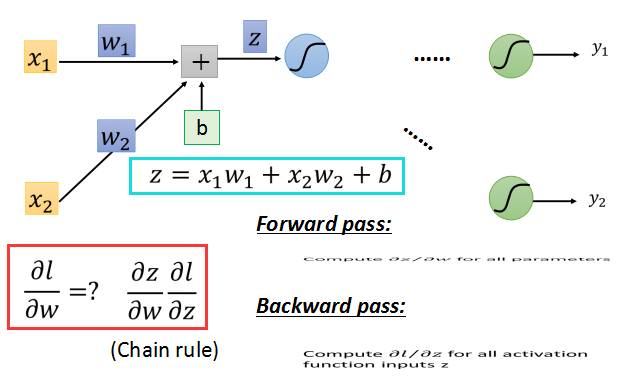
如上面的红框中所示，根据链式法则，l对w的偏导数，等于z对w的偏导数乘以l对z的偏导数。

l对w的梯度可以分为两部分：

前向传播：对所有参数求梯度；

后向传播：对所有激活函数的输入z求梯度；

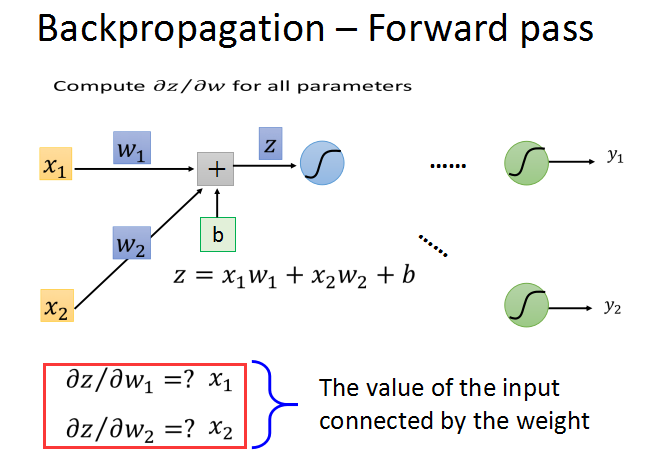
前向传播的梯度求法简单，就前一层的输入z对w求偏导数，直接求出就是对应的输入x_i。

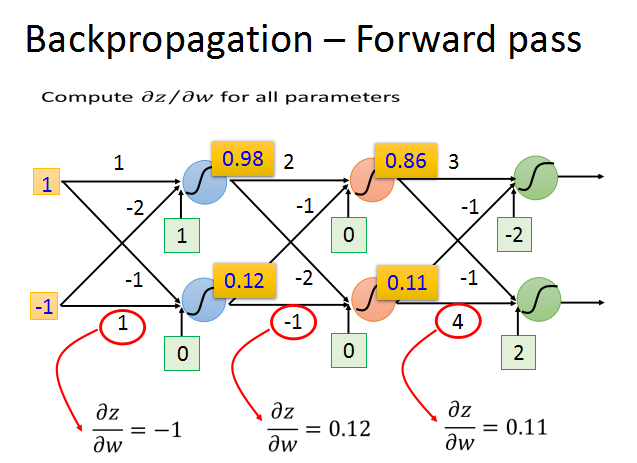
只要知道了激活函数的输出值，就可以轻易算出z/w的梯度，这个过程就是前向传播。

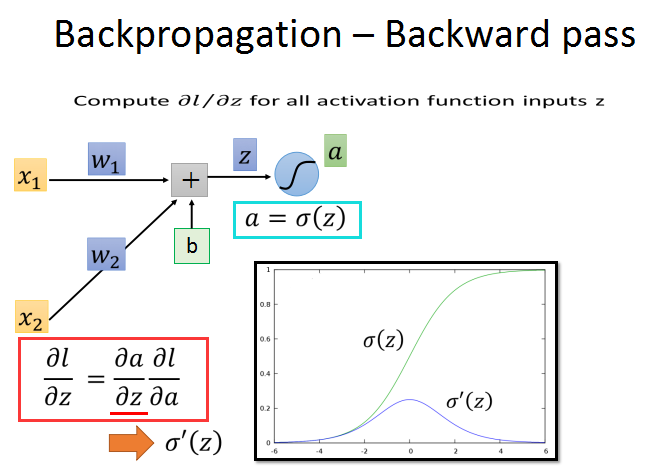
后向传播比较复杂，需要再使用链式法则，如红框中所示。l/z的梯度分解为a/z和l/a的梯度。

z对应当前节点的输入，a对应当前节点的输出。

a对z的导数图像如上所示，现在关键就是求l对a的偏导数。

为了求出l对a的偏导数，继续使用链式法则，关联上后面的两个神经元。

a通过z’和z''间接影响l，l/a的梯度应该是它所连接的所有神经元的梯度之和，不止是上面说的两项。

z'/a和z''/a的偏导数根据前向传播计算，分别是w3和w4.

现在问题就转化成了，求红框中的两个问号的梯度/

现在假设两个问号梯度已知，就可以求出之前l对z的梯度了。

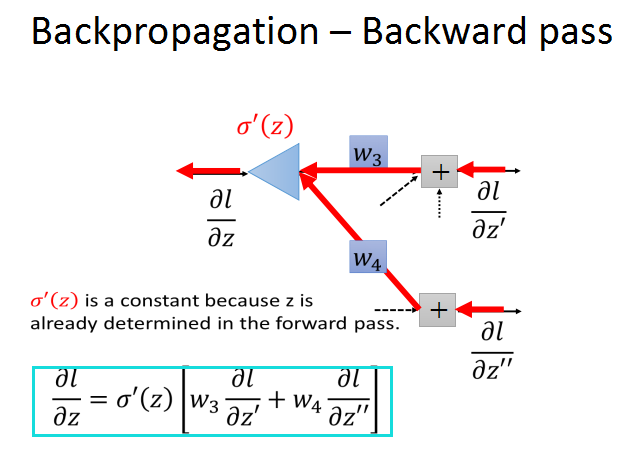
这样看上去有形成了一个新的网络，一个新的neural，输入是l/z'和l/z''的梯度,分别乘上对应权重w3，w4，

经过激活函数(乘以sigma(z)的导数)的作用，输出l/z的梯度。

现在来看看怎么可以求出l对z的梯度。

第一种情况：当z‘和z’‘为输出层时。根据链式法则，y/z的梯度可以根据对应的激活函数算出了，l/y的梯度是根据Cost function算出来的，这样问题就解决了。

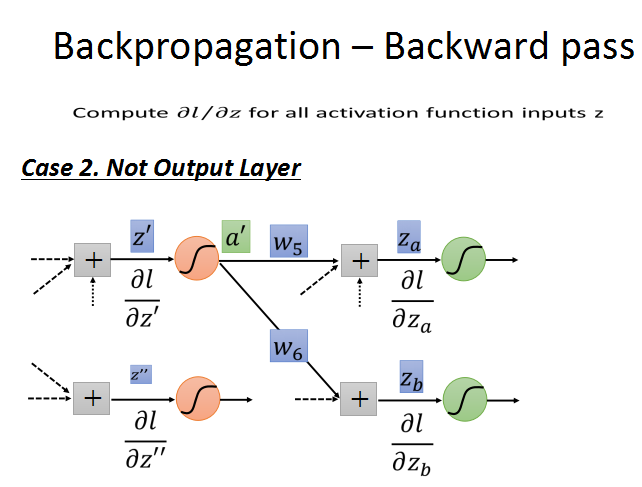
第二种情况：不是输出层。就是说还有后续的神经元节点连接，往后继续使用链式法则求导，直至输出层。

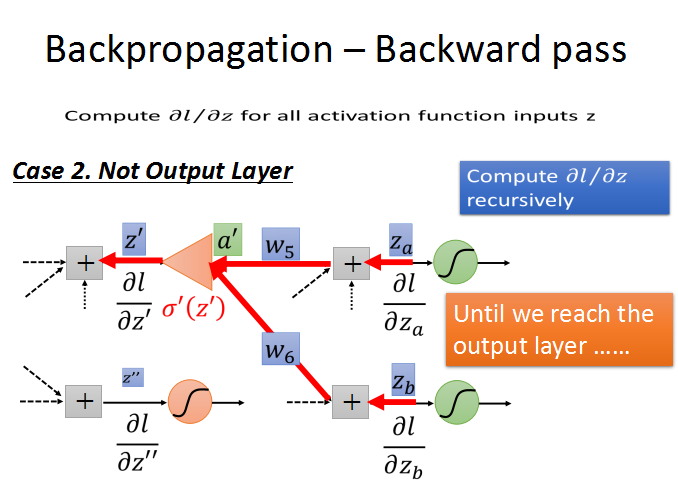
循环计算l对z的梯度，直到输出层，出现case1的情况，问题也就解决了。

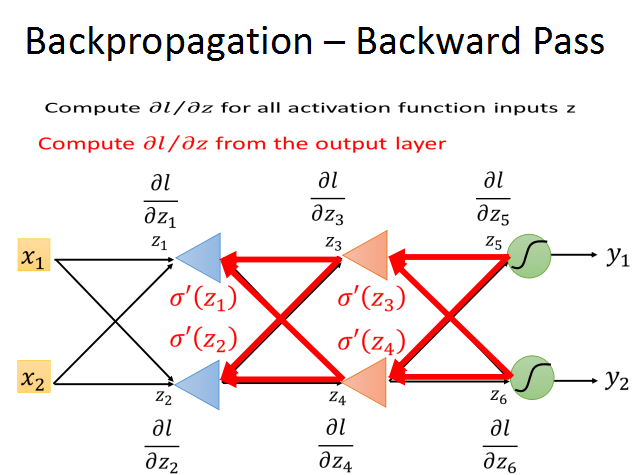
所以，我们就可以从输出层开始，反向计算l对每层z的梯度，在结合前向传播得到的梯度，就可以计算出梯度下降所需的梯度了。

而且，反向传播的复杂度和前向传播是一样的，这样就大大提升了梯度计算的效率。后一层的梯度，乘以相应的w，相加再乘上σ‘(z)，就得到了当前层的l/z的梯度。

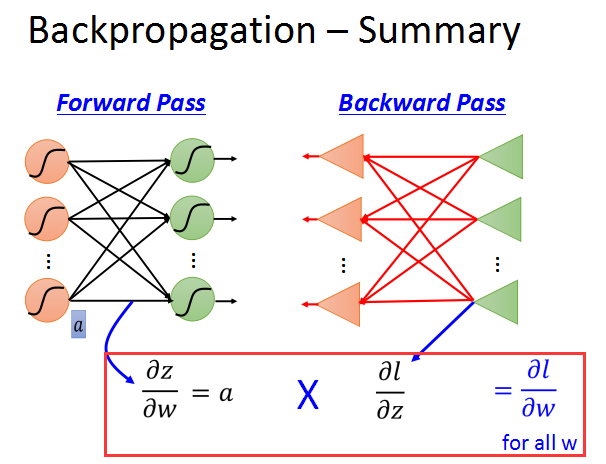
最后结果就是这样的：