Codeforces Round #283 (Div. 2) A ,B ,C 暴力，暴力，暴力

A. Minimum Difficulty

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Mike is trying rock climbing but he is awful at it.

There are n holds on the wall, i-th hold is at height ai off the ground. Besides, let the sequence ai increase, that is, ai < ai + 1 for all ifrom 1 to n - 1; we will call such sequence a track. Mike thinks that the track a1, ..., an has difficulty 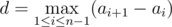. In other words, difficulty equals the maximum distance between two holds that are adjacent in height.

Today Mike decided to cover the track with holds hanging on heights a1, ..., an. To make the problem harder, Mike decided to remove one hold, that is, remove one element of the sequence (for example, if we take the sequence (1, 2, 3, 4, 5) and remove the third element from it, we obtain the sequence (1, 2, 4, 5)). However, as Mike is awful at climbing, he wants the final difficulty (i.e. the maximum difference of heights between adjacent holds after removing the hold) to be as small as possible among all possible options of removing a hold. The first and last holds must stay at their positions.

Help Mike determine the minimum difficulty of the track after removing one hold.

Input

The first line contains a single integer n (3 ≤ n ≤ 100) — the number of holds.

The next line contains n space-separated integers ai (1 ≤ ai ≤ 1000), where ai is the height where the hold number i hangs. The sequence ai is increasing (i.e. each element except for the first one is strictly larger than the previous one).

Output

Print a single number — the minimum difficulty of the track after removing a single hold.

Examples

input

3
1 4 6

output

5

input

5
1 2 3 4 5

output

2

input

5
1 2 3 7 8

output

4

Note

In the first sample you can remove only the second hold, then the sequence looks like (1, 6), the maximum difference of the neighboring elements equals 5.

In the second test after removing every hold the difficulty equals 2.

In the third test you can obtain sequences (1, 3, 7, 8), (1, 2, 7, 8), (1, 2, 3, 8), for which the difficulty is 4, 5 and 5, respectively. Thus, after removing the second element we obtain the optimal answer — 4.

题意：依次只删掉2-（n-1) 的点，找到每次相邻的最大值，再找最大值里的最小值；

思路：暴力，直接贴代码；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
const int N=2e5+,M=1e6+,inf=1e9+,mod=1e9+;
int a[N];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
    }
    int ans=inf;
    for(int i=;i<n;i++)
    {
        int maxx=;
        for(int t=;t<=n;t++)
        {
            if(i==t)continue;
            if(i+==t)
                maxx=max(maxx,a[t]-a[t-]);
            else
                maxx=max(maxx,a[t]-a[t-]);

        }
        ans=min(ans,maxx);
    }
    printf("%d\n",ans);
    return ;
}

B. Secret Combination

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You got a box with a combination lock. The lock has a display showing n digits. There are two buttons on the box, each button changes digits on the display. You have quickly discovered that the first button adds 1 to all the digits (all digits 9 become digits 0), and the second button shifts all the digits on the display one position to the right (the last digit becomes the first one). For example, if the display is currently showing number 579, then if we push the first button, the display will show 680, and if after that we push the second button, the display will show 068.

You know that the lock will open if the display is showing the smallest possible number that can be obtained by pushing the buttons in some order. The leading zeros are ignored while comparing numbers. Now your task is to find the desired number.

Input

The first line contains a single integer n (1 ≤ n ≤ 1000) — the number of digits on the display.

The second line contains n digits — the initial state of the display.

Output

Print a single line containing n digits — the desired state of the display containing the smallest possible number.

Examples

input

3
579

output

024

input

4
2014

output

0142

题意：你可以让每个数+1，再循环让每个数向后移一位，求最小；

思路：暴力，n*n*10；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
const int N=2e5+,M=1e6+,inf=1e9+,mod=1e9+;
char a[N];
string s[N];
int main()
{
    int n;
    scanf("%d",&n);
    scanf("%s",a);
    for(int i=;i<n;i++)
    a[i+n]=a[i];
    a[*n]=;
    string minn="";
    for(int i=;i<n;i++)
    {
        s[i].clear();
        for(int t=i;t<i+n;t++)
        s[i]+=a[t];
        if(minn=="")
        minn=s[i];
        else if(minn>s[i])
        minn=s[i];
        for(int t=;t<=;t++)
        {
            for(int j=;j<n;j++)
            {
                s[i][j]+=;
                if(s[i][j]>'')
                s[i][j]-=;
            }
            if(minn>s[i])
            minn=s[i];
        }
    }
    cout<<minn<<endl;
    return ;
}

C. Removing Columns

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an n × m rectangular table consisting of lower case English letters. In one operation you can completely remove one column from the table. The remaining parts are combined forming a new table. For example, after removing the second column from the table

abcd
edfg
hijk

we obtain the table:

acd
efg
hjk

A table is called good if its rows are ordered from top to bottom lexicographically, i.e. each row is lexicographically no larger than the following one. Determine the minimum number of operations of removing a column needed to make a given table good.

Input

The first line contains two integers  — n and m (1 ≤ n, m ≤ 100).

Next n lines contain m small English letters each — the characters of the table.

Output

Print a single number — the minimum number of columns that you need to remove in order to make the table good.

Examples

input

1 10
codeforces

output

0

input

4 4
case
care
test
code

output

2

input

5 4
code
forc
esco
defo
rces

output

4

Note

In the first sample the table is already good.

In the second sample you may remove the first and third column.

In the third sample you have to remove all the columns (note that the table where all rows are empty is considered good by definition).

Let strings s and t have equal length. Then, s is lexicographically larger than t if they are not equal and the character following the largest common prefix of s and t (the prefix may be empty) in s is alphabetically larger than the corresponding character of t.

题意：n个单词，每次可以删除一列，使得n个单词字典序；

思路：暴力；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
const int N=1e2+,M=1e6+,inf=1e9+,mod=1e9+;
int n,m;
int flag[N];
string a[N];
int check(int x)
{
    string st[N];
    for(int i=;i<n;i++)
    {
        st[i].clear();
        for(int t=;t<=x;t++)
        if(!flag[t])
        st[i]+=a[i][t];
        if(i)
        {
            if(st[i]<st[i-])
            return ;
        }
    }
    return ;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<n;i++)
    cin>>a[i];
    int ans=;
    for(int i=;i<m;i++)
    {
        if(check(i)==)
        {
            flag[i]=;
            ans++;
        }
    }
    printf("%d\n",ans);
    return ;
}