Prim求MST最小生成树

最小生成树即在一个图中用最小权值的边将所有点连接起来。prim算法求MST其实它的主要思路和dijkstra的松弛操作十分相似

prim算法思想：
在图中随便找一个点开始这里我们假定起点为“1”，以点1为松弛点将与之相连接的点进行松弛操作并更新它们的dis值因为我们只需要连接它们的最短边因此我们只需要

"dis[ i ]=edges[pos][ i ]"(记录松弛点到与之相连的节点的边权) 接下来的操作和dijkstra一样我们进行贪心找到距松弛点最近的点并记录下它的坐标，而且使之成为下一个松弛点

然后我们循环n遍(一共n个节点) 最后它们的dis值就为构成一棵树的最短边。

图解：

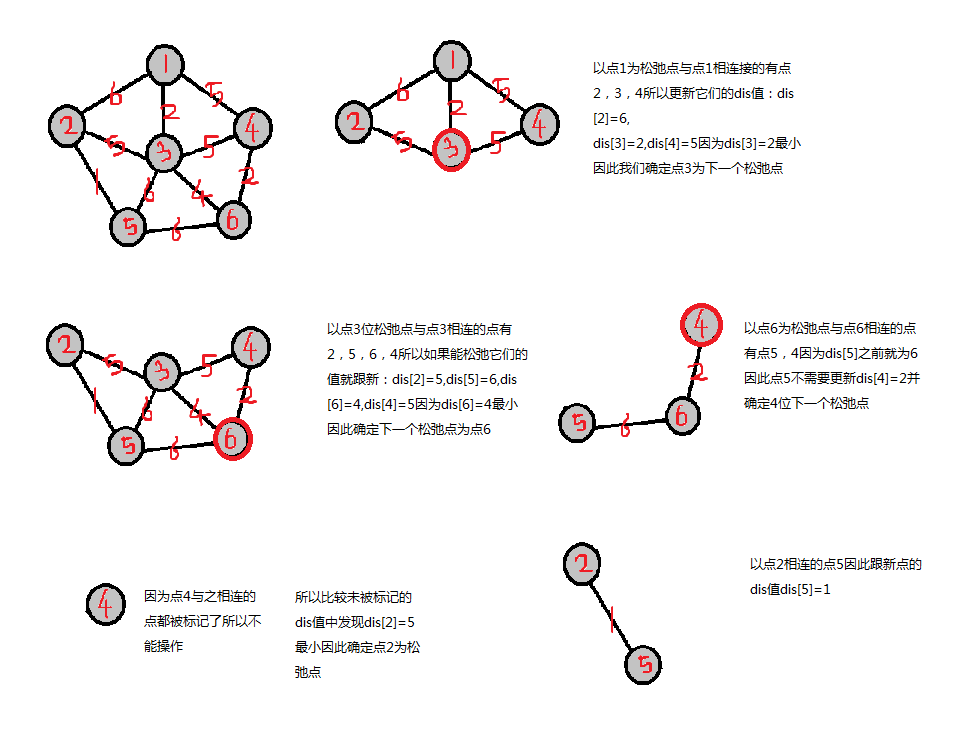
由上面的贪心过程可以得到prim的工作原理就是将所有点作为松弛点对每个点的最短连接边进行松弛因此这些边可以构成一棵最小的树

代码：

for(int k=;k<=n;k++)
{
     insert minn=INF,pos;
     for(int i=;i<=n;i++)
     {
          if(!vis[i]&&dis[i]<minn)//寻找松弛点
          {
              pos=i;
              minn=dis[i];
          }
     }
}

贪心代码：

for(int i=;i<=n;i++)
{
    if(!vis[i]&&dis[i]>edges[pos][i])//prim核心代码
    dis[i]=edges[pos][i];//贪心将每个点更新与之相连的最小的值
}

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdio>
#include <iomanip>
using namespace std;
typedef int insert;
#define in cin
const int INF=0x3f3f3f3f;
const int N=+;
insert edges[N][N],dis[N],vis[N];
insert n,m,x,y,z;
long long sum;
void value()
{
    memset(edges,INF,sizeof(edges));
    memset(dis,INF,sizeof(dis));
    for(int i=;i<=m;i++)
    {
        in>>x>>y>>z;
        if(edges[x][y]>z||edges[y][x]>z)
        {
            edges[x][y]=z;
            edges[y][x]=z;
        }
    }
    dis[]=;
    return;
}
void prim()
{
    for(int k=;k<=n;k++)
    {
        insert minn=INF,pos;
        for(int i=;i<=n;i++)
        {
            if(!vis[i]&&dis[i]<minn)
            {
                pos=i;
                minn=dis[i];
            }
        }
        vis[pos]=true;
        for(int i=;i<=n;i++)
        {
            if(!vis[i]&&dis[i]>edges[pos][i])
            dis[i]=edges[pos][i];
        }
    }
    return;
}
int main()
{
    in>>n>>m;
    value();
    prim();
    for(int i=;i<=n;i++)
       sum+=dis[i];
       cout<<"最小生成树的总权值"<<endl;
       cout<<sum<<endl;
       cout<<"每个点的最短边"<<endl;
       for(int i=;i<=n;i++)
       cout<<dis[i]<<" ";
    return ;
}

但是如果用邻接矩阵存图既浪费空间又存不了大图所以便有了以下vector邻接表版本

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iomanip>
#include <vector>
#include <stack>
using namespace std;
typedef int insert;
#define in cin
#define out cout
const int INF=0x3f3f3f3f;
const int N=2e5+;
insert n,m,x,y,z,dis[N],sum,startpoint;
bool vis[N];
struct Node
{
    insert to,w;
};
vector<struct Node> vt[N];
void inital_value()
{
    memset(dis,INF,sizeof(dis));
    for(int i=;i<=m;i++)
    {
        cin>>x>>y>>z;
        struct Node now;
        now.to=y;now.w=z;
        vt[x].push_back(now);
        now.to=x;
        vt[y].push_back(now);
    }
    dis[startpoint]=;
    return;
}

void prim()
{
    for(int k=;k<=n;k++)
    {
        insert minn=INF,pos;
        for(int i=;i<=n;i++)
        {
            if(!vis[i]&&dis[i]<minn)
            {
                minn=dis[i];
                pos=i;
            }
        }
        vis[pos]=true;
        for(int i=;i<vt[pos].size();i++)
        {
            if(!vis[vt[pos][i].to]&&dis[vt[pos][i].to]>vt[pos][i].w)
            dis[vt[pos][i].to]=vt[pos][i].w;
        }
    }
    return;
}
int main()
{
    in>>n>>m>>startpoint;
    inital_value();
    prim();
    for(int i=;i<=n;i++)
    sum+=dis[i];
    for(int i=;i<=n;i++)
    cout<<startpoint<<"-->"<<i<<" "<<dis[i]<<endl;
    cout<<"最小生成树的总边权："<<endl;
    cout<<sum<<endl;
    return ;
}