LibreOJ 6002 最小路径覆盖(最大流)
题解:最小路径覆盖=总点数减去最大匹配数,拆点,按照每条边前一个点连源点,后一个点连汇点跑最大流,即可跑出最大匹配数,然后减一减就可以了~
代码如下:
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x3f3f3f3f
#define hi puts("hi");
using namespace std; int head[],next[],v[],w[],deep[];
int s,t,cnt; void init()
{
cnt=-;
memset(head,-,sizeof(head));
memset(next,-,sizeof(next));
} void add(int from,int to,int cost)
{
cnt++;
next[cnt]=head[from];
w[cnt]=cost;
v[cnt]=to;
head[from]=cnt;
} void add_edge(int from,int to,int cost)
{
add(from,to,cost);
add(to,from,);
} int bfs(int s,int t)
{
queue<int> q;
memset(deep,,sizeof(deep));
deep[s]=;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=head[u];i!=-; i=next[i])
{
if(w[i]>&&(!deep[v[i]]))
{
deep[v[i]]=deep[u]+;
q.push(v[i]); //
}
}
}
if(!deep[t])
{
return ;
}
return ;
} int dfs(int u,int t,int dist)
{
if(u==t)
{
return dist;
}
for(int i=head[u]; i!=-; i=next[i])
{
if(w[i]&&(deep[v[i]]==deep[u]+))
{
int di=dfs(v[i],t,min(w[i],dist));
if(di>)
{
w[i]-=di;
w[i^]+=di;
return di;
}
}
}
return ;
} int dinic(int s,int t)
{
int res=;
while(bfs(s,t))
{
while(int d=dfs(s,t,inf))
{
res+=d;
}
}
return res;
} int n,m;
int vis[]; int solve(int x,int &f)
{
int loc=x+n;
vis[x]=;
for(int i=head[loc];i!=-;i=next[i])
{
if(w[i]==&&v[i]!=n*+)
{
solve(v[i],f);
}
}
if(f==)
{
f=;
}
else
{
putchar(' ');
}
printf("%d",x);
} int main()
{
scanf("%d%d",&n,&m);
init();
s=;t=n*+;
for(int i=;i<=n;i++)
{
add_edge(s,i,);
add_edge(i+n,t,);
}
int x,y;
while(m--)
{
scanf("%d%d",&x,&y);
add_edge(x,y+n,);
}
int ans=n-dinic(s,t);
for(int i=head[t];i!=-;i=next[i])
{
if(w[i]==&&!vis[v[i]-n])
{
int f=;
solve(v[i]-n,f);
puts("");
}
}
printf("%d\n",ans);
}
LibreOJ 6002 最小路径覆盖(最大流)的更多相关文章
- 洛谷 P2764 LibreOJ 6002 最小路径覆盖问题
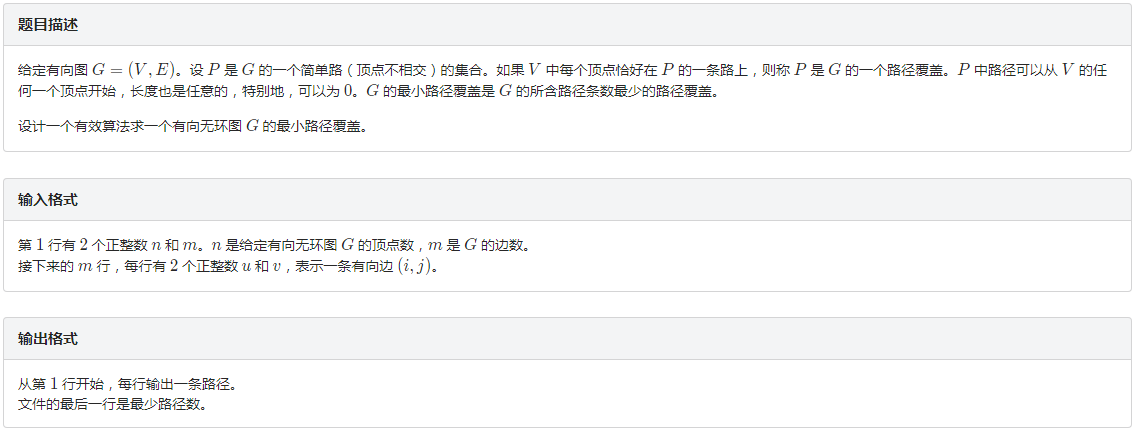
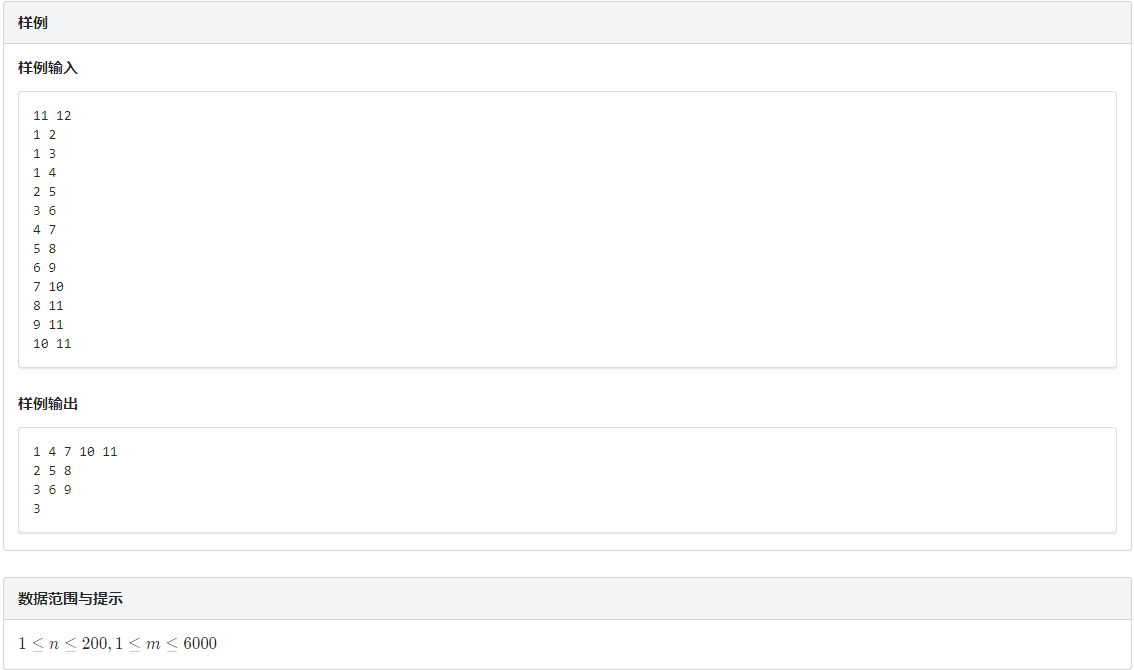
题目描述 «问题描述: 给定有向图G=(V,E).设P 是G 的一个简单路(顶点不相交)的集合.如果V 中每个顶点恰好在P 的一条路上,则称P是G 的一个路径覆盖.P 中路径可以从V 的任何一个顶点开 ...
- Loj 6002 最小路径覆盖(最大流)
题意: 求不相交的最小路径覆盖 思路: 连边跑二分图,匹配一条边相当于缩了一条边,答案为n-maxflow 如果是求可以相交的最小路径覆盖的话,先用Floyd跑出可达矩阵,然后所有可达的点连边跑二分图 ...
- [SDOI2010][bzoj1927] 星际竞速 [最小路径覆盖+费用流]
题面 传送门 思路 仔细观察题目要求的东西,发现就是求一个最小路径覆盖,只不过可以跳跃(就是那个鬼畜的超级跳跃) 那么就直接上最小路径覆盖模版 对每个点,拆成两个点$X_i$和$Y_i$,建立超级源超 ...
- 网络流24题 第三题 - CodeVS1904 洛谷2764 最小路径覆盖问题 有向无环图最小路径覆盖 最大流 二分图匹配 匈牙利算法
欢迎访问~原文出处——博客园-zhouzhendong 去博客园看该题解 题目传送门 - CodeVS1904 题目传送门 - 洛谷2764 题意概括 给出一个有向无环图,现在请你求一些路径,这些路径 ...
- Luogu 2764 最小路径覆盖问题 / Libre 6002 「网络流 24 题」最小路径覆盖 (网络流,最大流)
Luogu 2764 最小路径覆盖问题 / Libre 6002 「网络流 24 题」最小路径覆盖 (网络流,最大流) Description 给定有向图G=(V,E).设P是G的一个简单路(顶点不相 ...
- LibreOJ #6002. 「网络流 24 题」最小路径覆盖
#6002. 「网络流 24 题」最小路径覆盖 内存限制:256 MiB时间限制:1000 ms标准输入输出 题目类型:传统评测方式:Special Judge 上传者: 匿名 提交提交记录统计讨论测 ...
- 【wikioi】1904 最小路径覆盖问题(最大流+坑人的题+最小路径覆盖)
http://wikioi.com/problem/1904/ 这题没看数据的话是一个大坑(我已报告官方修复了),答案只要求数量,不用打印路径...orz 最小路径覆盖=n-最大匹配,这个我在说二分图 ...
- BZOJ.1927.[SDOI2010]星际竞速(无源汇上下界费用流SPFA /最小路径覆盖)
题目链接 上下界费用流: /* 每个点i恰好(最少+最多)经过一次->拆点(最多)+限制流量下界(i,i',[1,1],0)(最少) 然后无源汇可行流 不需要源汇. 注: SS只会连i',求SS ...
- 洛谷 P2764 最小路径覆盖问题【最大流+拆点+路径输出】
题目链接:https://www.luogu.org/problemnew/show/P2764 题目描述 «问题描述: 给定有向图G=(V,E).设P 是G 的一个简单路(顶点不相交)的集合.如果V ...
随机推荐
- Spring启动后获取所有拥有特定注解的Bean,注解的属性值
最近项目中遇到一个业务场景,就是在Spring容器启动后获取所有的Bean中实现了一个特定接口的对象,第一个想到的是ApplicationContextAware,在setApplicationCon ...
- MFC调试的几个技巧
TCHAR pStr[] = _T("this is a test!"); void* p = (void*)pStr; TRACE(_T("pStr is %s\n&q ...
- 给安卓端调用的apk、图片下载接口
package com.js.ai.modules.pointwall.action; import java.io.File; import java.io.FileInputStream; imp ...
- php代码执行漏洞
php代码执行的两个函数eval(),assert() <?php $i = $_GET['x']; eval($i); ?> eval()函数将以php类型执行传入的参数x的值 给x传入 ...
- Deep Learning 学习笔记(1):线性回归( Linear Regression )
关于DL,由于我是零经验入门, 事实上我是从最简单的ML开始学起, 所以这个系列我也从ML开始讲起. ===============并行分割线================= 一.线性回归 线性回归 ...
- Python not readable
try: with open('data.txt','w') as f: for each_line in f: print(each_line)except OSError as reason: p ...
- 自定义inputformat和outputformat
1. 自定义inputFormat 1.1 需求 无论hdfs还是mapreduce,对于小文件都有损效率,实践中,又难免面临处理大量小文件的场景,此时,就需要有相应解决方案 1.2 分析 小文件的优 ...
- BeX5 常见问题解决办法
1.获取当前Activity的名称 Activity activity = ProcessUtils.getActivityInProcessContext(); String activityNam ...
- SQL Where 字符串拼接
) set @s='1,2,3' --法一: --法二: exec('select * from tb where id in ('+@s+')')
- 【原】Coursera—Andrew Ng机器学习—Week 1 习题—Linear Regression with One Variable 单变量线性回归
Question 1 Consider the problem of predicting how well a student does in her second year of college/ ...
