Leetcode solution 124: Binary Tree Maximum Path Sum

Problem Statement

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example 1:

Input: [1,2,3]

       1
      / \
     2   3

Output: 6

Example 2:

Input: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

Output: 42

Problem link

Video Tutorial

You can find the detailed video tutorial here

• Youtube
• B站

Thought Process

When dealing with binary tree related problem, traversals using recursion is our friend. It seems we can perform a post-order traversal, and keep track of the maximum sums.

If the path has to go through root, then in each post-order step, we will have the max_sum_of_the_left_path, max_sum_of_the_right_path, the current_node_value, we simply return and record

single_path_max = max(the current_node_value, max(max_sum_of_the_left_path, max_sum_of_the_right_path) + current_node_value)

However, the problem allows a path that not goes through the root, therefore, we need to also record a max between left + current node value + right, i.e.,

global_max = max(single_path_max, max_sum_of_the_left_path + current_node_value + max_sum_of_the_right_path)

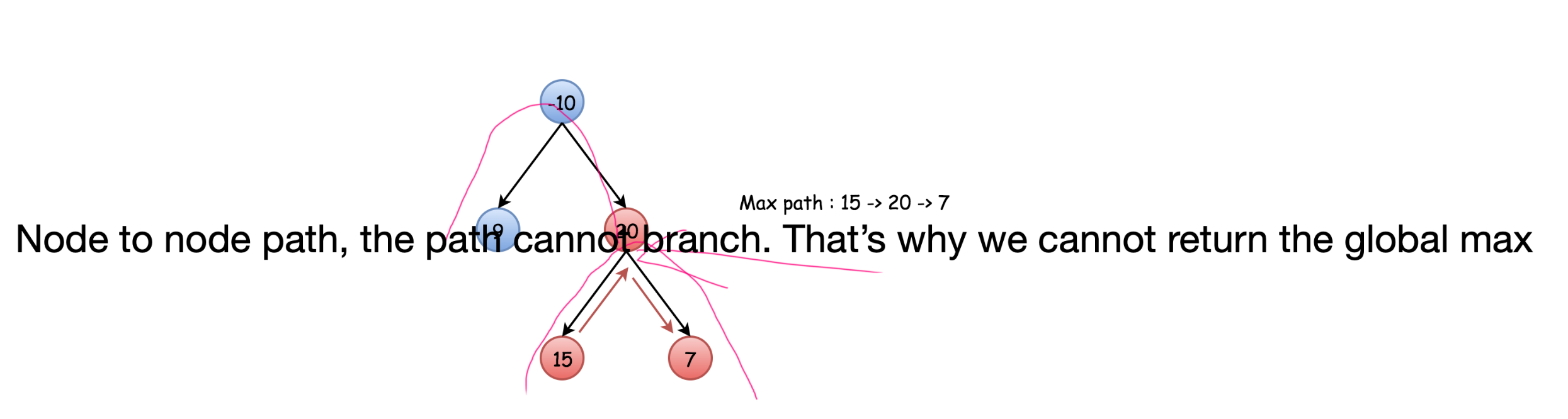
One caveat is in your recursion, we should still return the single_path_max. The reason we should not return the global_max is in that case, it will not be a single node to single node path.

Solutions

Post-order recursion

 private int max = Integer.MIN_VALUE;

 public int maxPathSum(TreeNode root) {
     maxPathSumHelper(root);
     return this.max;
 }

 public int maxPathSumHelper(TreeNode root) {
     if (root == null) {
         return 0;
     }

     int left = maxPathSumHelper(root.left);
     int right = maxPathSumHelper(root.right);

     // the max on a single path
     int singlePath = Math.max(root.val, Math.max(left, right) + root.val);
     // max across the current node on two sides
     int acrossPath = Math.max(singlePath, left + right + root.val);
     if (acrossPath > this.max) {
         this.max = acrossPath;
     }

     // Note: always want to return the single path for recursion, because you cannot include both path, else,
     // it will not be a path
     return singlePath;
 }

Time Complexity: O(N), each node is visited once

Space Complexity:No extra space is needed other than the recursion function stack

References

• Leetcode official solution