MIT线性代数:4.A的LU分解



MIT线性代数:4.A的LU分解的更多相关文章
- 线性代数之——A 的 LU 分解
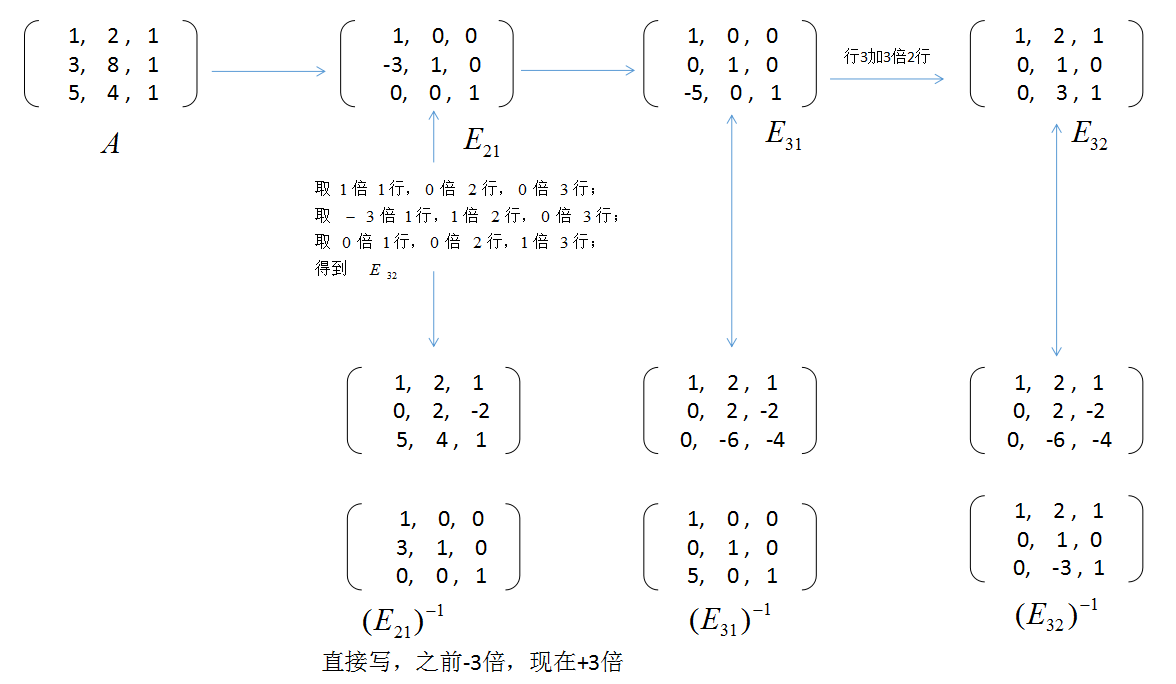
1. A = LU 之前在消元的过程中,我们看到可以将矩阵 \(A\) 变成一个上三角矩阵 \(U\),\(U\) 的对角线上就是主元.下面我们将这个过程反过来,通一个下三角矩阵 \(L\) 我们可以 ...
- 线性代数笔记10——矩阵的LU分解
在线性代数中, LU分解(LU Decomposition)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积).LU分解主要应用在数值分析 ...
- 矩阵LU分解分块算法实现
本文主要描述实现LU分解算法过程中遇到的问题及解决方案,并给出了全部源代码. 1. 什么是LU分解? 矩阵的LU分解源于线性方程组的高斯消元过程.对于一个含有N个变量的N个线性方程组,总可以用高斯消去 ...
- matlab 求解线性方程组之LU分解
线性代数中的一个核心思想就是矩阵分解,既将一个复杂的矩阵分解为更简单的矩阵的乘积.常见的有如下分解: LU分解:A=LU,A是m×n矩阵,L是m×m下三角矩阵,U是m×n阶梯形矩阵 QR分解: 秩分解 ...
- MIT线性代数课程 总结与理解-第一部分
概述 个人认为线性代数从三个角度,或者说三个工具来阐述了线性关系,分别是: 向量 矩阵 空间 这三个工具有各自的一套方法,而彼此之间又存在这密切的联系,通过这些抽象出来的工具可以用来干一些实际的活,最 ...
- 矩阵分解---QR正交分解,LU分解
相关概念: 正交矩阵:若一个方阵其行与列皆为正交的单位向量,则该矩阵为正交矩阵,且该矩阵的转置和其逆相等.两个向量正交的意思是两个向量的内积为 0 正定矩阵:如果对于所有的非零实系数向量x ,都有 x ...
- LU分解,Javascript代码
///A 为矩阵,这里写成一维数组,如 [1],[1,2,3,4] function GetLU(a) { var n = a.length;//矩阵的总数据数目 var s = Math.sqrt( ...
- matlab实现高斯消去法、LU分解
朴素高斯消去法: function x = GauElim(n, A, b) if nargin < 2 for i = 1 : 1 : n for j = 1 : 1 : n A(i, j) ...
- LU分解(2)
接着上次LU分解的讲解,这次给出使用不同的计算LU分解的方法,这种方法称为基于GaxPy的计算方法.这里需要了解lapapck中的一些函数.lapack中有一个函数名为gaxpy,所对应的矩阵计算公式 ...
- LU分解(1)
1/6 LU 分解 LU 分解可以写成A = LU,这里的L代表下三角矩阵,U代表上三角矩阵.对应的matlab代码如下: function[L, U] =zlu(A) % ZLU ...
随机推荐
- 数据库系统概论——从E-R模型到关系模型
E-R模型和关系模型都是现实世界抽象的逻辑表示 E-R模型并不被 DBMS直接支持,更适合对现实世界建模 关系模型是 DBMS直接支持的数据模型 基本 E-R图中的元素包括实体集.联系集.属性 椭圆框 ...
- [Note] 使用Code Snippet简化编码
使用NewtonSoft.Json写实体类时大量格式一致的代码出现 ,这时可以使用Code snippet来加快编码速度 [JsonProperty(PropertyName = "mess ...
- Java 学习笔记之 线程interrupt方法
线程interrupt方法: interrupt方法是用来停止线程的,但是他的使用效果并不像for+break那样,马上就停止循环. 调用interrupt()其实仅仅是在当前线程中打了一个停止标记, ...
- LitePal的修改和删除操作
转载出处:http://blog.csdn.net/guolin_blog/article/details/40083685 传统的修改和删除数据方式 上篇文章中我们已经得知,SQLiteData ...
- mac下的环境变量
a. /etc/profile b. /etc/paths c. ~/.bash_profile d. ~/.bash_login e. ~/.profile f. ~/.bashrc 其中a和b是系 ...
- 机器学习实战_KNN(一)
[是什么] KNN 即 k_近邻算法(k- nearest neighbor) ,就是寻找K个邻居作为该样本的特征,近朱者赤,近墨者黑,你的邻居是什么特征,那么就认为你也具备该特征:核心公式为: 数据 ...
- 浅谈爬虫 《一》 ===python
浅谈爬虫 <一> ===python ‘’正文之前先啰嗦一下,准确来说,在下还只是一个刚入门IT世界的菜鸟,工作近两年了,之前做前端的时候就想写博客来着,现在都转做python了,如果还 ...
- c++11::std::decltype/declval
decltype ( 实体 ) () (C++ 起) decltype ( 表达式 ) () (C++ 起) 若实参是其他类型为 T 的任何表达式,且 a) 若 表达式 的值类别为亡值,则 declt ...
- 简单理解TCP通信的三次握手
TCP是主机对主机层的传输控制协议,提供可靠的连接服务,采用三次握手确认建立一个连接. 位码(可以理解为请求状态): 有6种标示:SYN(synchronous建立联机) ACK(acknowledg ...
- QCustomplot使用分享(九) 绘制图表-多功能游标
目录 一.概述 二.效果图 三.源码讲解 1.源码结构 2.头文件 3.添加游标 4.监测移动 5.移动游标 6.其他函数 四.测试方式 1.测试工程 2.测试文件 3.测试代码 五.相关文章 六.总 ...
