P4799 [CEOI2015 Day2]世界冰球锦标赛（折半暴搜）

题目很明确，不超过预算的方案数。两个直觉：1、暴搜2、dp

每个点两种状态，选或不选....

1、可过20%

2、可过70%

正解：折半搜索（meet in the middle）

有点像以前的双向广搜，原理其实是很像的，为了省略很多状态的枚举。

如果暴搜的话应该是O（2^n），n<=40，而折半搜的话，理论复杂度是O（2^（n/2）），看到一张图很好地诠释了优化复杂度&&空间的原理

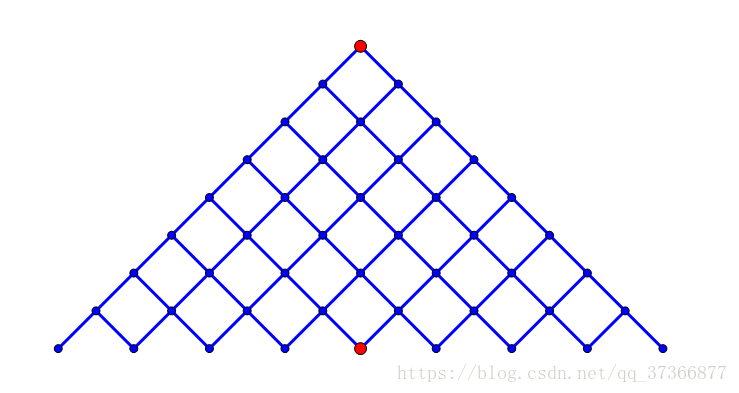
（此为暴搜）

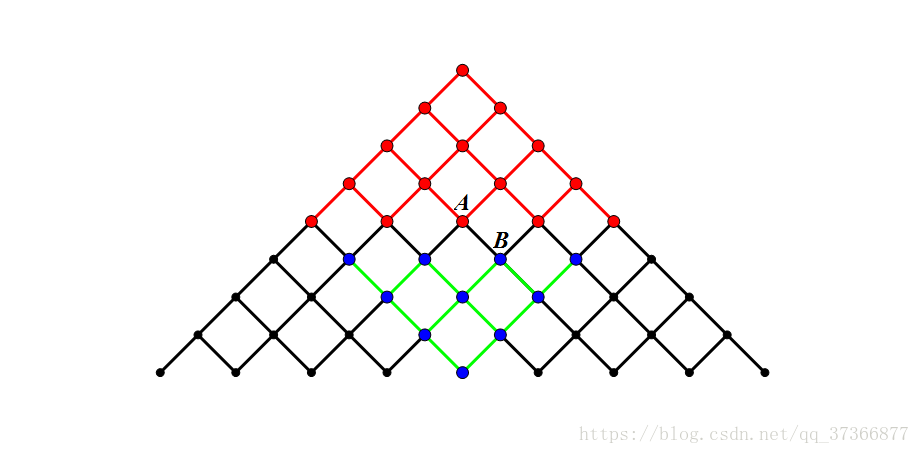
（感谢顾哥NET这位大佬的图）

于是，分两次dfs，把答案记录在两个数组里。

问题在于，怎么统计答案。

a数组里，记录的是每一个可能答案在左区间搜索到的累加值（不超过m的值），右区间相同。要把两者加起来判断。

• 可以n^2，在此题和没有差不多

但是还有更好的方法;

对两个分别排序(O(2log(n/2))，这时对于每一个b【i】，都可以在a中找到一个点a【pos】，使得pos前的点+p【i】都不超过n，所以就可以愉快地使用upper_bound了。

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn=1e6+1e5;
ll n,m;
ll a[maxn];
ll b[maxn];
ll w[maxn];
void dfs(ll l,ll r,ll &now,ll a[],ll num)
{
    if(num>m)
    return;
    if(l>r)
    {
        a[++now]=num;
        return;
    }
    dfs(l+,r,now,a,num+w[l]);
    dfs(l+,r,now,a,num);
}
ll suma,sumb;
ll ans;
/*
5 1000
100 1500 500 500 1000
*/
ll mid;
int main()
{
    scanf("%lld%lld",&n,&m);
    for(int i=;i<=n;i++)
    {
        scanf("%lld",&w[i]);
    }
    mid=n>>;
    dfs(,mid,suma,a,);
    dfs(mid+,n,sumb,b,);
    sort(a+,a+suma+);
    for(int i=;i<=sumb;i++)
    {
        ans+=upper_bound(a+,a+suma+,m-b[i])-a-;
    }
    printf("%lld",ans);
    return ;
}

应该算是折半搜索的板子题了，升级版请见（传送门）

（完）