一文搞懂transform: skew

目录

• 理解坐标系
• 复合变换

如何理解斜切 skew，先看一个 demo。在下面的 demo 中，有 4 个正方形，分别是

红色：不做 skew 变换，

绿色：x 方向变换，

蓝色：y 方向变换，

黑色：两个方向都变换，

拖动下面的滑块可以查看改变 skew 角度后的效果。切换 selector 可以设置 transform-origin，origin 默认是 0% 0%。大家可以把玩一下。

如果你把滑块拖到了 90deg 或者 - 90deg，那么你应该可以回答上面的问题了。如果你在 chrome 上看到整个页面变白，可以到隔壁 firefox 上试试，就这个 demo 而言，火狐是表现最好的, safari 最差。

See the Pen skew by imgss
(@imgss) on CodePen.

用左扭，右扭来理解 skew 可能更加符合我们的直觉，但是却是不准确的。拿绿色正方形来说，origin 在 0% 0% 时，skew 20 度看起来像是往右扭，但是 origin 变成 100% 100% 时，看起来又像是往左扭了。

那么到底该怎么理解这个 skew 变换呢，其实它是矩阵 matrix 变换的一种。关于矩阵变换，张鑫旭老师的这篇文章讲解的不错，传送门，其中提到 skew 变化和通用 matrix 变换的对应关系：

也就是说 matrix 函数的第二三个参数来控制图形的斜切的，更通用一点，下面这个图展示了 css matrix 中的 6 个参数分别控制哪种变换，我们可以看一下：

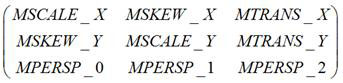
写到 matrix 函数里面如下：

有同学问了，为什么没有旋转的参数啊，其实旋转是 scale 和 skew 的组合操作。但是为了保证旋转后和原来的形状保持一致，4 个参数应该存在如下关系：

换句话说，旋转是一组特定的 scale + skew 组合操作。

理解坐标系

在了解到 skew 其实是一种矩阵变换后，我们来了解一下浏览器里的坐标系。因为除了 transform，其他操作都受坐标原点的影响。在浏览器中，向下为 Y 轴正方向，向右为 x 轴正方向，唯独原点是不确定的，而这正是 transform-origin 所起的作用。

当你设置这个属性为 top left 时，就是说矩阵变换坐标系的原点位于左上角，从而得到图形中的各个点的坐标，通过矩阵运算得到变换后的坐标，最后由浏览器渲染出来。设置为 50% 50% 则意味着坐标原点在图形的中心。

复合变换

思考下面两行 css:

对两个个正方形分别做上述变换，出来的效果是不同的，原因是因为上面两个操作，相当于对坐标进行两次矩阵乘法运算，不同于普通的乘法运算，矩阵乘法运算是不存在 ** 交换率 ** 的，所以结果会不同。

参考文章：

https://www.cnblogs.com/TianFang/p/3920734.html

https://code-industry.net/masterpdfeditor-help/transformation-matrix/

https://www.zhangxinxu.com/wordpress/2012/06/css3-transform-matrix-矩阵/

https://blog.csdn.net/u012964944/article/details/77824768

https://www.jianshu.com/p/956d54376338