数据结构与算法(1)支线任务3——Largest Rectangle in Histogram

题目如下：(https://leetcode.com/problems/largest-rectangle-in-histogram/)

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

        

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3]. The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,
Given height = [2,1,5,6,2,3],
return 10.

题目似乎很简单，只要求出直方图中最大的矩形面积即可。然而最最单纯的O(n²)算法显然会跪（别人试过，我就不作死了……）。

有两类思路，分别如下：

Part One

提示说用栈，然而并没有想出如何使用。看懂别人的思路后再写，总觉得略微无聊……还是在此用自己的话复述一下吧。

（以下所有图片来自http://blog.csdn.net/doc_sgl/article/details/11805519）

题目要求需要找面积最大的矩形，这个矩形的高为直方图中某柱高，我们可以认为矩形是由一个柱向两侧扩展得到的。

题中的直方图可以形象地理解为“波”，在一个波峰附近第一个高度下降的柱（下图中的t）会限制其左侧比它高的柱（记某柱为z）形成矩形的宽度，又由于t是该波峰第一个下降的柱形，故左侧比它高的柱z形成的矩形宽度为t与z横坐标之差（由于后续操作形成的波并不是连续的柱，此处实际上应为t-z前一个柱横坐标-1），这样就得到了一个矩形面积。

如上操作后，柱z已经完成了它的使命（已经求出由它形成的矩形的面积，左右的矮柱也不需要它的高度），当t左侧所有高柱都完成使命后，t成了相对高的柱，可以看作与前面的更矮的柱又在形成一个又矮又宽的波峰（图中阴影），遇到更矮的i之后，重复前面的操作即可得到所有柱生成的矩形的面积。

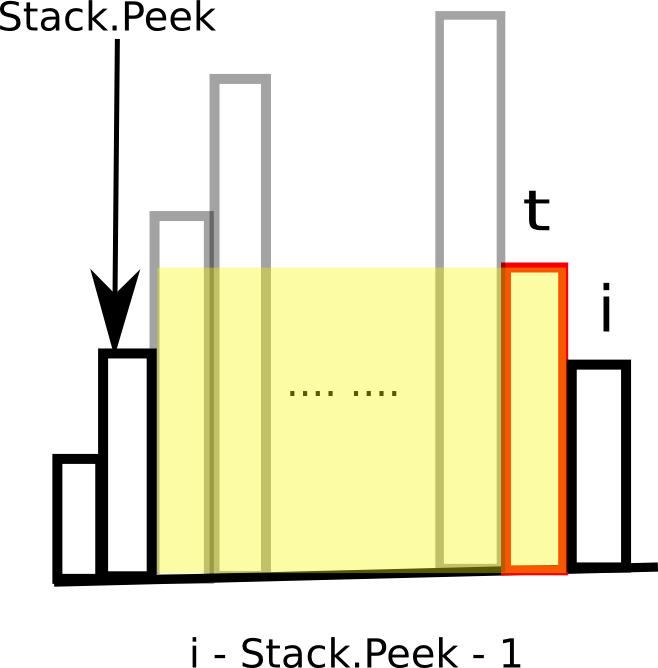
于是，我们可以用栈保存一串连续上升的柱（波上升的部分），当遇到矮柱时，求前面每个高柱形成的矩形的面积，然后将这个没用的高柱弹出。最后将矮柱压入，作为下一个波的上升部分。这个过程扫描一遍，算法复杂度为O(n)。

/************************如果觉得上面写的清晰可以忽略下面的部分**************************/

针对样例输入，可以进行如下分析：

1.将柱0压栈，。

2.柱1更矮，求柱0形成的矩形面积，将柱1压栈。

3.柱1柱2柱3高度递增，进栈。

4.柱4比2,3矮：柱3求面积，出栈；柱2求面积，出栈。

5.柱4柱5进栈。

6.最后求栈中剩余柱形成矩形的面积（相当于最后有一个高度为0的柱，使其前面的柱出栈）。

（似乎应该在这里再说一下，以上所有图片来自http://blog.csdn.net/doc_sgl/article/details/11805519 ）//2015/11/13日补

/************************懂了上面，下面的代码其实不重要了**************************/

class Solution {
public:
    int largestRectangleArea(vector<int>& height) {

        height.push_back(); //使最后栈中剩余柱出栈
        stack<int> serHeight; //储存高度递增的柱的栈
        int maxArea = ; //最大面积
        int curArea = ; //当前矩形面积

        for (int i = ; i < height.size(); i++)
        {
            if (serHeight.empty() || height[serHeight.top()] <= height[i]) //高度上升，进栈
            {
                serHeight.push(i);
            }
            else
            {
                //将高矩形出栈，求其生成的矩形面积
                while (height[serHeight.top()] > height[i])
                {
                    int cur = serHeight.top();
                    serHeight.pop();
                    if (serHeight.empty())
                    {
                        curArea = height[cur] * i;
                        maxArea = (maxArea > curArea) ? maxArea : curArea;
                        break;
                    }
                    curArea = height[cur] * (i - serHeight.top() - );
                    maxArea = (maxArea > curArea) ? maxArea : curArea;
                }

                serHeight.push(i);
            }
        }
        return maxArea;
    }
};

Part Two

一个更容易想到的思路是先判断每个柱左右两边不比它矮的最远柱，然后可以更容易地算出由当前柱形成的矩形面积。

利用动态规划的思想，可以利用前面已确定的最远高柱更新当前需要找的柱。比如下面代码中若l[i]左边的l[i]-1比i还要高，那么可以用l[l[i] - 1]更新l[i]，这样可以加快查找高柱的速度。

class Solution {
public:
    int largestRectangleArea(vector<int>& height) {
        int maxArea = ; //最大面积
        int curArea = ; //当前面积
        int s = height.size(); //柱形个数
        int *l = new int[s]; //储存不比当前柱矮的最左端柱
        int *r = new int[s]; //储存不比当前柱矮的最右端柱

        //先找储存不比当前柱矮的最左端柱
        for (int i = ; i < s; i++)
        {
            l[i] = i; //自己不比自己矮
            //利用已存过的l[i]判断是否找到最左端
            while (l[i] && height[l[i] - ] >= height[i])
            {
                l[i] = l[l[i] - ];
            }
        }
        //再找储存不比当前柱矮的最右端柱
        for (int i = s - ; i >= ; i--)
        {
            r[i] = i;
            while ((r[i] - s + ) && height[r[i] + ] >= height[i])
            {
                r[i] = r[r[i] + ];
            }
        }
        //计算由当前柱生成的矩形面积，更新最大面积
        for (int i = ; i < s; i++)
        {
            curArea = height[i] * (r[i] - l[i] +);
            maxArea = (maxArea > curArea) ? maxArea : curArea;
        }

        return maxArea;
    }
}

附：

日常膜：http://www.cnblogs.com/lustralisk/p/branch-3.html

生日快乐：http://blog.sina.com.cn/s/blog_1495db3970102w3f8.html