PCurve - Curve on Surface

eryar@163.com

Abstract. 本文通过给出曲面上曲线PCurve的定义来对OpenCascade中的Curve On Surface进行理解，并介绍了OpenCascade对应的类BRep_CurveOnSurface实现。通过Tcl脚本输出的球的拓朴信息，分析PCurve的实际应用。

Key words. OpenCascade, ACIS, PCurve, Curve on Surface, Parametric Surface

1. Introduction

不管是ACIS还是OpenCascade中都有PCurve这个概念，字面上来理解就是参数曲线（Parametric Curve）。在《基于ACIS的几何造型技术与系统开发》中也看到这个概念，如下图所示：

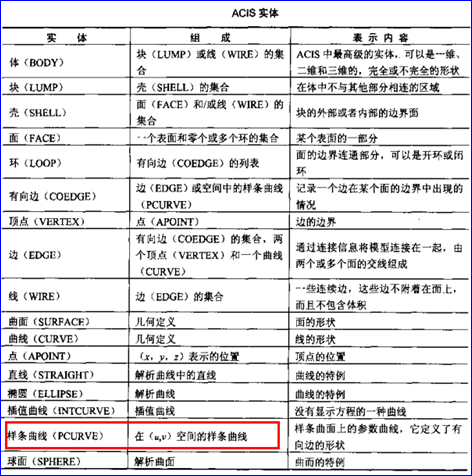
Figure 1.1 PCurve Entity of ACIS

“参数空间曲线是在参数曲面的双参数空间中的二维样条曲线。类pcurve是附加在参数曲面之间公共边上的数据结构。”看完之后，对pcurve的概念还是不太清楚。本文给出PCurve的定义，并介绍PCurve在OpenCascade中的实现。根据定义可以对PCurve有个基本认识。

2. Definition of PCurve

PCurve为曲面上的曲线（Curve on Surface），其定义为：设曲面方程为

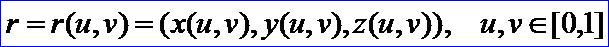
令参数u,v又是另一参数t的函数，即

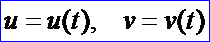
将其代入曲面方程，得到：

当t变化时，就得到曲面上的一条单参数曲线，称为曲面上的曲线或简称曲面上曲线（Curve on Surface）。若以s表示曲面上曲线的弧长，则由复合函数的求导公式可得弧长微分公式：

令：

则有：

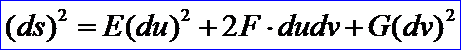
在古典微分几何中，上式称为曲面的第一基本公式，E，F，G称为第一基本量。在曲面上，每一点的第一基本量与参数化无关，在整张曲面上，第一基本量是参数u和v的连续函数。读者注意，弧元ds是曲线的几何不变量，与曲面的参数化无关。关于曲线曲面更多的信息，请参考《微分几何》、《计算几何》之类的书籍。本文主要为了理解曲面上曲线PCurve的概念及其在OpenCascade中的实现。

目前对PCurve的应用还不太清楚，但是微分几何中引入这个概念肯定是有他的意义，就像在程序设计中引入Pimpl（pointer to implementation）这个idiom。尽管引入Pimpl idiom会增加内存的额外开销，甚至因为增加了间接层使程序代码变得不易读和不好调试，但是人们仍然乐于使用。站在API设计者的角度，它能隐藏信息、降低耦合、减少文件间的依赖，加快编译速度、且可使生成的库的兼容性更好等等，很多优点。所以在《Effective C++》和《API Design for C++》中，作者反复提到并使用Pimpl idiom。类比微分几何引入的PCurve，先在此做上标记，如果有了新的理解再做分析。

3. PCurve in OpenCascade

在OpenCascade中对应于曲面上曲线PCurve的类是BRep_CurveOnSurface，其文档中的说明为：Representation of a curve by a curve in the parametric space of a surface.

结合定义上面这句话就好理解了。现摘抄部分代码来分析PCurve的定义和使用：

//=======================================================================

//function : BRep_CurveOnSurface

//=======================================================================

BRep_CurveOnSurface::BRep_CurveOnSurface(const Handle(Geom2d_Curve)& PC,

                     const Handle(Geom_Surface)& S,

                     const TopLoc_Location& L) :

       BRep_GCurve(L,PC->FirstParameter(),PC->LastParameter()),

       myPCurve(PC),

       mySurface(S)

{

}

//=======================================================================

//function : D0

//=======================================================================

void BRep_CurveOnSurface::D0(const Standard_Real U, gp_Pnt& P) const

{

  // shoud be D0 NYI

  gp_Pnt2d P2d = myPCurve->Value(U);

  P = mySurface->Value(P2d.X(),P2d.Y());

  P.Transform(myLocation.Transformation());

}

从其构造函数来看，要生成一个PCurve必须有曲线PC和曲面S及位置L。

从求PCurve的零次微分的函数D0可以看出，只需要一个参数U就可以计算出曲面上的点P。结合前面介绍的PCurve的定义，不难理解这段代码的意义。下面通过分析球面的拓朴结构，看看PCurve的应用。

Figure 3.1 Sphere in Draw Test Harness

4. Code Demo

下面的程序生成一个球，再把其拓朴结构显示出来，可以看到其中就有PCurve的信息。使用Tcl脚本程序示例如下：

pload ALL

psphere s 1.0

dump s

以上Tcl脚本在OpenCascade的Draw Test Harness中运行结果如下所示：

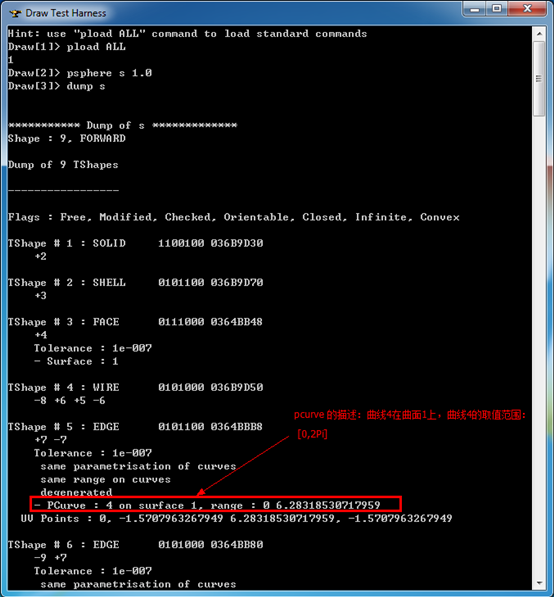
Figure 4.1 PCurve in Sphere

由上图可知，球的Edge5由一个PCurve来表示。曲面上曲线PCurve在拓朴结构输出的信息位于Curve2ds中，曲面的几何数据位于surfaces中，分别如下图所示：

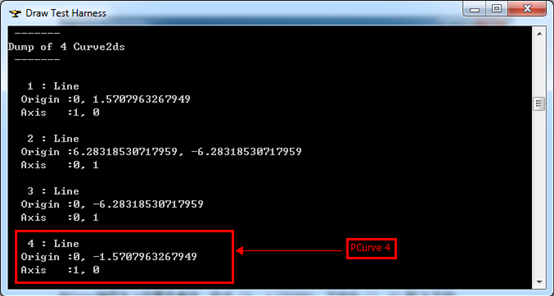
Figure 4.2 PCurves of Sphere

PCurve编号为4的是条直线，起点（0，-1.570796），方向为（1，0）即X方向。

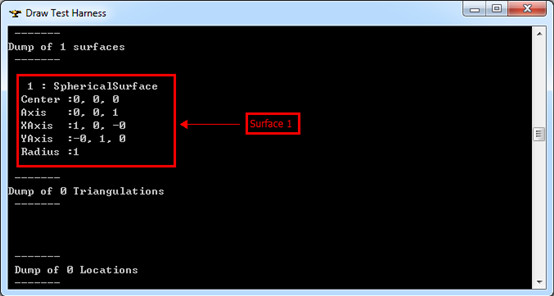
Figure 4.3 Surfaces of Sphere

曲面编号为1的是一个球面，圆心（0，0，0），半径为1，坐标系与世界坐标系相同。

结合PCurve 4和曲面1及PCurve的参数范围，可以计算出曲面上的一条曲线上的坐标值。不过上面球面的例子中的Edge是degenerated边，退化成一个点了。

由上面球的拓朴信息可知，在理解了参数曲线曲面（有向性）、奇点（Singular Point），参数曲面的奇异性（Singularity）、曲面上曲线（PCurve）等概念后，OpenCascade的拓朴结构就可以基本理解了。

5. Conclusions

本文通过给出曲面上曲线PCurve的定义来对OpenCascade中的Curve On Surface进行理解，并介绍了OpenCascade对应的类BRep_CurveOnSurface实现。

通过Tcl脚本输出的球的拓朴信息，看看PCurve的实际应用，从中可以看出使用Tcl的简单与便捷。

6. References

1. 朱心雄，自由曲线曲面造型技术，科学出版社，2000

2. 王仁宏李崇君朱春钢，计算几何教程，科学出版社，2008

3. 陈维桓，微分几何，北京大学出版社，2006

4. 詹海生李广鑫马志欣，基于ACIS的几何造型技术与系统开发，清华大学出版社，2002

PDF Version: PCurve - Curve on Surface