LCA（最近公共祖先）算法

参考博客：https://blog.csdn.net/my_sunshine26/article/details/72717112

首先看一下定义，来自于百度百科

　　LCA（Lowest Common Ancestors），即最近公共祖先，是指在有根树中，找出某两个结点u和v最近的公共祖先。

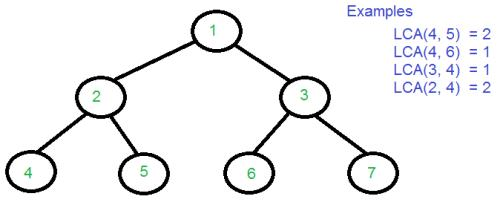
注意：这里某个节点本身也是它的祖先节点。

求最近公共祖先的算法：

1、暴力：每次查询的时间复杂度为O(N)

2、Tarjan（离线）算法：在一次遍历中把所有查询解决，预处理时间复杂度O(nlogn),每次查询时间复杂度O(1)，总时间复杂度是O(nlogn+q)

3、倍增算法：利用二分两个节点同时往上走，直到相遇，预处理时间复杂度O(nlogn)，每次查询时间复杂度O(logn)

Tarjan（离线）算法

一.Tarjan算法大致实现过程

1. 先选择一个节点u为根节点，从根节点开始搜索。（标记u已访问过）
2. 遍历该点u的所有儿子节点v，并标记v已访问过。
3. 若v还有儿子节点，对v重复ii操作，否则进入下一操作。
4. 把v合并到u上（并查集）。
5. 把当前的点设为u，遍历与u有询问关系的节点v。
6. 如果v在之前已经被访问过，那么u和v的最近公共祖先就是v通过并查集合并后的父亲节点（注意是合并后），即当前的find（v）。

 

 

二.Tarjan算法的伪代码

　　

 Tarjan(u)           //根节点u
 {
     for each(u,v)
     {
         Tarjan(v);  //v还有儿子节点
         join(u,v);  //把v合并到u上
         vis[v]=;   //访问标记
     }
     for each(u,v)   //遍历与u有询问关系的节点v
     {
         if(vis[v])
         {
             ans=find(v);
         }
     }
 }

三.Tarjan算法的代码

 void Tarjan(int u)
 {
     vis[u]=;
     for(int i=;i<mp[u].size();i++)
     {
         int v=mp[u][i];
         if(vis[v]==)
         {
             Tarjan(v);
             join(u,v);
         }
     }
     for(int i=;i<mp2[u].size();i++)//利用mp2集合来存储查询关系
     {
         int v=mp2[u][i];
         if(vis[v]==)
         {
             lca[u][v]=find(v);
         }
     }
 }

倍增算法

一、算法铺垫

首先让u和v中较深的一个往上走|depth(u)-depth(v)|步，然后再一起一步步往上走，直到走到同一个节点，就可以在O(depth(u)+depth(v))的时间内求出LCA。

关键在于如何优化向上查找的过程

二.倍增算法的实现过程

分析刚才的算法，两个节点到达同一节点后，不论怎么向上走，达到的显然还是同一节点。利用这一点，我们就能够利用二分搜索求出到达最近公共祖先的最小步数了。

首先我们要进行预处理。对于任意的节点，可以通过fa2[v]=fa[fa[v]]得到其向上走2步到达的顶点，再利用这个信息，又可以通过fa4[v]=fa2[fa2[v]]得到其向上走4步所到的顶点。以此类推，我们可以得到其向上走2^k步所到的顶点fa[v][k],预处理的时间点复杂度为O(nlogn)。

 void init()
 {
     lg[]=;
     for(int i=;i<=n;i++)
       lg[i]=lg[i-]+(<<(lg[i-]+)==i);//用来求log2(n)
 }
 void dfs(int f,int fath)
 {
     deepth[f]=deepth[fath]+;
     fa[f][]=fath;
     for(int i=;(<<i)<=deepth[f];i++)
       fa[f][i]=fa[fa[f][i-]][i-];
     for(int i=;i<mp[f].size();i++)
       if(mp[f][i]!=fath)
         dfs(mp[f][i],f);
 }
 int lca(int x,int y)
 {
     if(deepth[x]<deepth[y])
       swap(x,y);
     while(deepth[x]>deepth[y])
       x=fa[x][lg[deepth[x]-deepth[y]]];
     if(x==y)
       return x;
     for(ll k=lg[deepth[x]];k>=;k--)
       if(fa[x][k]!=fa[y][k])
         x=fa[x][k], y=fa[y][k];
     return fa[x][];
 }