OpenCV学习(30) 轮廓defects

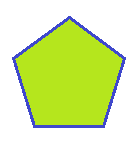
上一篇教程中，我们学习了如何计算轮廓的凸包，其实对一个轮廓而言，可能它的凸包和它本身是重合的，也有可能不是重合的。比如下面左边图像的轮廓本身就是凸包，而右边图像的轮廓则不是。我们可以通过函数bool isContourConvex(InputArray contour)，来判定一个轮廓是否是凸包，是的话返回true，否则false[注意测试的轮廓必须是简单轮廓，没有自交叉之类的]。

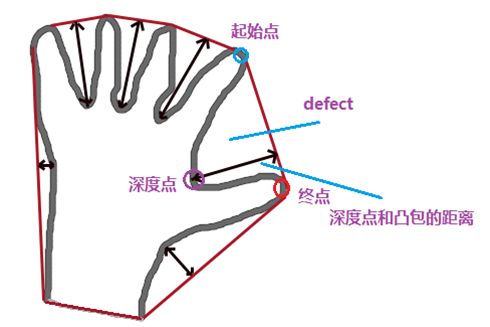
对一个非凸包的轮廓而言，它包括一系列的凹陷区域，这些区域称作defect，比如下面手轮廓中，包括6个defect区域。在OpenCV中，我们用下面的结构来定义defect。

struct CvConvexityDefect { CvPoint* start; // 轮廓中defect的起点 CvPoint* end; // 轮廓中defect的终点 CvPoint* depth_point; // defect中到凸包最远的点 float depth; // 最远点和凸包之间的距离};

在OpenCV中，我们通过函数

void convexityDefects(InputArray contour, InputArray convexhull, OutputArray convexityDefects)

得到轮廓的凸包，其中第一个参数和第二个参数是轮廓以及轮廓对应的凸包，注意凸包应该使用vector<int>这样的索引方式表示。第三个参数为返回的defect点集。

下面我们看下检测轮廓defects的代码：

#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <iostream>
#include <stdio.h>
#include <stdlib.h>

using namespace cv;
using namespace std;

Mat src; Mat src_gray;
RNG rng(12345);

int main( int argc, char** argv )
{
    //装入图像
    src = imread("../hand1.jpg", 1 );

    //转化为灰度图像
    cvtColor( src, src_gray, CV_BGR2GRAY );
    //blur( src_gray, src_gray, Size(3,3) );
    namedWindow( "image");
    imshow( "image", src_gray );

    Mat threshold_output;
    vector<vector<Point> > contours;
    vector<Vec4i> hierarchy;

    //得到二值图
    threshold( src_gray, threshold_output, 200, 255, THRESH_BINARY );

    //查找轮廓
    findContours( threshold_output, contours, hierarchy, CV_RETR_TREE, CV_CHAIN_APPROX_SIMPLE, Point(0, 0) );
    printf("轮廓数目:%d\n", contours.size());
    /// Find the convex hull object for each contour
    vector<vector<Point> >hull( contours.size() );
    for( int i = 0; i < contours.size(); i++ )
    {  convexHull( Mat(contours[i]), hull[i], false ); }

    /// Draw contours + hull results
    Mat drawing = Mat::zeros( threshold_output.size(), CV_8UC3 );
    int area = 0; //轮廓索引
    int k = 0;
    int i;
    for(i = 0; i< contours.size(); i++ )
    {
        Scalar color1 = Scalar( rng.uniform(0, 255), rng.uniform(0,255), rng.uniform(0,255) );
        drawContours( drawing, contours, i, color1, 1, 8, vector<Vec4i>(), 0, Point() );
        Scalar color2 = Scalar( rng.uniform(0, 255), rng.uniform(0,255), rng.uniform(0,255) );
        drawContours( drawing, hull, i, color2, 1, 8, vector<Vec4i>(), 0, Point() );
        int tt = contourArea(contours[i]);
        printf("轮廓面积%d = %d\n", i, tt);
        if( tt > area)
        {
            area = contourArea(contours[i]);
            k = i;
        }

    }

    vector<Point> hull1;
    hull1 = hull[1];
    for(i = 0; i< hull1.size(); i++ )
    {
        printf("point %d, %d, %d\n", i, hull1[i].x, hull1[i].y);
        circle(drawing, hull1[i], 6, Scalar(255,0,0), 3, CV_AA);  
    }

    int j;
    for(j=0; j< contours.size(); j++)
    {
        //如果没有defects或者轮廓小于三个点，则continue
        if( isContourConvex(contours[j])|| contours[j].size()<3) continue;

        vector<int> convexHull_IntIdx;
        vector<Vec4i> defects;
        if (contours[j].size() >3 )
        {
            convexHull(contours[j], convexHull_IntIdx, true);
            convexityDefects(contours[j], convexHull_IntIdx, defects);
        }    

        for(i=0;i < defects.size();++i)  
        {  
            Matx<int,4,1> defectVector = defects[i];
            vector<Point> contours1 =contours[j];
            Point point1 = contours1[defectVector.val[0]];//开始点
            Point point2 = contours1[defectVector.val[1]];//结束点
            Point point3 = contours1[defectVector.val[2]];//深度点
            float dist = defectVector.val[3];
            printf("dist: %f \n", dist);
            //if ( defectVector.val[3] <= 1000 ) { continue; } // skip defects that are shorter than 100 pixel
            circle(drawing, point1, 3, Scalar(255,255,0), 2, CV_AA);
            circle(drawing, point2, 8, Scalar(0,255,0), 2, CV_AA);
            circle(drawing, point3, 3, Scalar(0,255,255), 2, CV_AA);

        }  
    }
    /// Show in a window
    namedWindow( "Hull demo");
    imshow( "Hull demo", drawing );

    waitKey(0);
    return(0);
}

程序执行之后界面如下，注意左下有图中

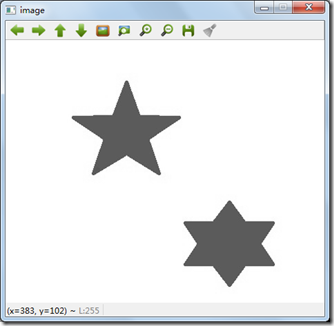
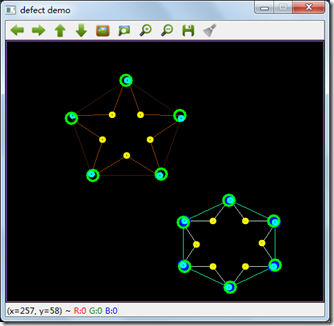
程序代码：工程FirstOpenCV25