c语言数字图像处理（六）：二维离散傅里叶变换

基础知识

复数表示

C = R + jI

极坐标：C = |C|(cosθ + jsinθ)

欧拉公式：C = |C|e^jθ

有关更多的时域与复频域的知识可以学习复变函数与积分变换，本篇文章只给出DFT公式，性质，以及实现方法

二维离散傅里叶变换(DFT)

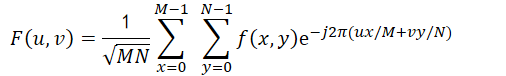
其中f(x,y)为原图像，F(u,v)为傅里叶变换以后的结果，根据欧拉公式可得，每个F(u,v)值都为复数，由实部和虚部组成

代码示例

 void dft(short** in_array, double** re_array, double** im_array, long height, long width)
 {
     double re, im, temp;

     for (int i = ; i < height; i++){
         for (int j = ; j < width; j++){
             re = ;
             im = ;

             for (int x = ; x < height; x++){
                 for (int y = ; y < width; y++){
                     temp = (double)i * x / (double)height +
                            (double)j * y / (double)width;
                     re += in_array[x][y] * cos(- * pi * temp);
                     im += in_array[x][y] * sin(- * pi * temp);
                 }
             }

             re_array[i][j] = re;
             im_array[i][j] = im;
         }
     }
     printf("dft done\n");
 }

傅里叶谱

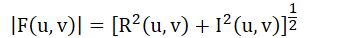
相角

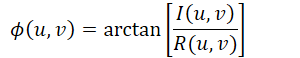
功率谱

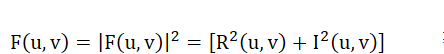
傅里叶变换频谱图

对于上面得两幅图案，在区间[0, M-1]中，变换数据由两个在点M/2处碰面的背靠背的半个周期组成

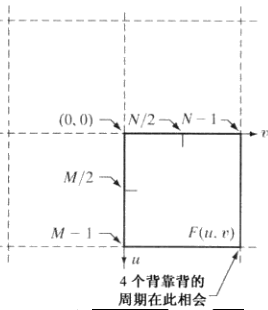
针对显示和滤波的目的，在该区间中有一个完整的变换周期更加方便，因为完整周期中数据是连续的

我们希望得到上图所示的图案

傅里叶变换的平移性质

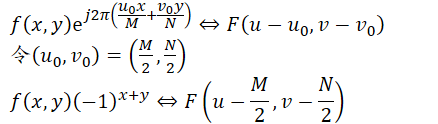
因此对每个f(x, y)项乘以(-1)^x+y可达目的

代码示例

 void fre_spectrum(short **in_array, short **out_array, long height, long width)
 {
     double re, im, temp;
     int move;

     for (int i = ; i < height; i++){
         for (int j = ; j < width; j++){
             re = ;
             im = ;

             for (int x = ; x < height; x++){
                 for (int y = ; y < width; y++){
                     temp = (double)i * x / (double)height +
                            (double)j * y / (double)width;
                     move = (x + y) %  ==  ?  : -;
                     re += in_array[x][y] * cos(- * pi * temp) * move;
                     im += in_array[x][y] * sin(- * pi * temp) * move;
                 }
             }

             out_array[i][j] = (short)(sqrt(re*re + im*im) / sqrt(width*height));
             if (out_array[i][j] > 0xff)
                 out_array[i][j] = 0xff;
             else if (out_array[i][j] < )
                 out_array[i][j] = ;
           }
     }
 }

执行结果

旋转性质

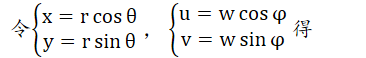
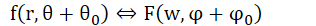
即f(x, y)旋转一个角度，F(u, v)旋转相同的角度

二维离散傅里叶反变换

代码示例

 void idft(double** re_array, double** im_array, short** out_array, long height, long width)
 {
     double real, temp;

     for (int i = ; i < height; i++){
         for (int j = ; j < width; j++){
             real = ;

             for (int x = ; x < height; x++){
                 for (int y = ; y < width; y++){
                     temp = (double)i * x / (double)height +
                            (double)j * y / (double)width;

                     real += re_array[x][y] * cos( * pi * temp) -
                             im_array[x][y] * sin( * pi * temp);
                 }
             }

             out_array[i][j] = (short)(real / sqrt(width*height));
             if (out_array[i][j] > 0xff)
                 out_array[i][j] = 0xff;
             else if (out_array[i][j] < )
                 out_array[i][j] = ;
         }
     }
     printf("idft done\n");
 }

经验证，图像经傅里叶变换，然后再反变换以后可恢复原图

改进

本篇文章只是按照二维离散傅里叶变换公式进行了实现，在测试的过程中发现，执行速度真的是非常慢，算法时间复杂度O(n⁴)，等以后有时间再对这段代码进行优化。