[九省联考 2018]IIIDX

Description

给你 $n+1$ 个节点的一棵树，节点编号为 $0\sim n$ ， $0$ 为根。边集为 $\mathbb{E}=\left\{(u,v)\big|\forall i\in[1,n],\left(\left\lfloor\frac{i}{k}\right\rfloor,i\right)\right\}$ 。给出 $n$ 个待选序号，让你为 $1\sim n$ 这 $n$ 个节点编号，第 $i$ 号节点编为 $a_i$，要求父亲编号小于等于儿子的编号。求满足要求的序列 $a_1,a_2,\cdots,a_n$ 中字典序最大的一个。

$1\leq n\leq 500000$

Solution

直接递归贪心回溯时选一个未选的最大值是错的。

考虑为什么会出错，依旧举一个例子：

4 2
1 1 1 2

画成图就是：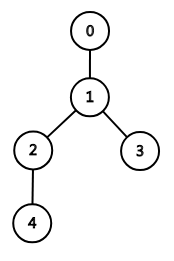

如果按照刚才的贪心方式，我们会先将 $2$ 赋给 $4$ 号节点，再将 $1$ 赋给 $2$ 号节点。这样就错了，考虑为什么？

因为容易发现，不论怎么分配， $2$ 号节点一定只能赋为 $1$ ，这时被选的数中有两个 $1$ ，等于说我们可以让 $4$ 号点取 $1$ ，这样是更优的。

那么之前的贪心就错了，但不过它提供了一个思路，就是对于一个节点的儿子们，一定是先尽可能将标号小的儿子的子树用大的标号标。唯一需要处理的就是子树的根节点的标号可能有多个相同的备选。

我们将被选数从大到小排序。一个节点按之前的方式编号，我们就要选与这个编号相同的最靠右的一个。这样能保证最优。

我们不用递归，我们只需要枚举节点时为其子树预留节点即可。

考虑线段树维护这样的一个数组 $f$ ，$f_i$ 表示 $i$ 位置前有多少个数可选。

每次查询的时候只要找到这样的一个最靠左的位置 $x$ ，使得 $\forall i,f_i\geq size_i$ ，其中 $size_i$ 为当前节点子树的大小。

然后将 $x$ 赋为与这个编号相同的最靠右的一个的位置。那么这个位置的值就是被选值。

处理完之后，我们还要对 $x$ 之后的 $f$ 数组进行修改。

以上操作都可以用线段树维护。

值得注意的是由于处理到一个节点的时候，如果它有父亲，那么要将其父亲的预留的额度删去。

如果仍有不理解，可参见ppt。

Code

#include <bits/stdc++.h>

using namespace std;

const int N = 500000+5;

int n, a[N], fa[N], nxt[N], size[N], ans[N]; double k;

struct Segment_tree {

#define lr(o) (o<<1)

#define rr(o) (o<<1|1)

    int minn[N<<2], tag[N<<2];

    void pushdown(int o) {

        minn[lr(o)] += tag[o], tag[lr(o)] += tag[o];

        minn[rr(o)] += tag[o], tag[rr(o)] += tag[o];

        tag[o] = 0;

    }

    void build(int o, int l, int r) {

        if (l == r) {minn[o] = l; return; } int mid = (l+r)>>1;

        build(lr(o), l, mid), build(rr(o), mid+1, r);

        minn[o] = min(minn[lr(o)], minn[rr(o)]);

    }

    void update(int o, int l, int r, int a, int b, int k) {

        if (a <= l && r <= b) {minn[o] += k, tag[o] += k; return; }

        pushdown(o); int mid = (l+r)>>1;

        if (a <= mid) update(lr(o), l, mid, a, b, k);

        if (b > mid) update(rr(o), mid+1, r, a, b, k);

        minn[o] = min(minn[lr(o)], minn[rr(o)]);

    }

    int query(int o, int l, int r, int k) {

        if (l == r) return minn[o] >= k ? l : l+1;

        pushdown(o); int mid = (l+r)>>1;

        if (k <= minn[rr(o)]) return query(lr(o), l, mid, k);

        else return query(rr(o), mid+1, r, k);

    }

}T;

bool comp(const int &a, const int &b) {return a > b; }

void work() {

    scanf("%d%lf", &n, &k);

    for (int i = 1; i <= n; i++) scanf("%d", &a[i]); sort(a+1, a+n+1, comp);

    for (int i = n; i >= 1; i--) {

        nxt[i] = i, fa[i] = floor(1.*i/k);

        ++size[i]; size[fa[i]] += size[i];

        if (a[i] == a[i+1]) nxt[i] = nxt[i+1];

    }

    T.build(1, 1, n);

    for (int i = 1; i <= n; i++) {

        if (fa[i] && fa[i] != fa[i-1]) T.update(1, 1, n, ans[fa[i]], n, size[fa[i]]-1);

        int loc = nxt[T.query(1, 1, n, size[i])]; ans[i] = loc;

        T.update(1, 1, n, loc, n, -size[i]);

    }

    for (int i = 1; i <= n; i++) printf("%d ", a[ans[i]]);

}

int main() {work(); return 0; }