[Luogu4724][模板]三维凸包(增量构造法)

1.向量点积同二维，x1y1+x2y2+x3y3。向量叉积是行列式形式，(y1z2-z1y2,z1x2-x1z2,x1y2-y1x2)。

2.增量构造法：

　　1)首先定义，一个平面由三个点唯一确定。一个平面是有方向的，它的法向量只有一个方向（即逆时针相邻两向量的叉积的方向）。

　　2)初始时只有(p1,p2,p3)和(p3,p2,p1)两个平面（相当于两个方向相反的面组成了一个体积为0的凸包）

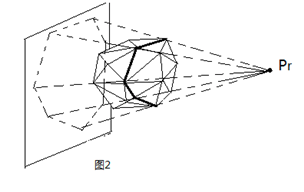
　　3)每次加入一个新点时，以这个点为光源中心投影到凸包上，不能被照到的面在新凸包中仍然存在，否则不存在。

　　4)将新点和明暗分界线上的边组成的面加入凸包。

3.具体实现：

　　1)一个面是否能被照到的判断：点在这个面的正面，即平面上任意一点到这个点的向量与平面法向量的点积为正值。

　　2)明暗分界线的判断：每次判断一个面能否被照到时，标记vis[p1][p2]表示p1p2这条边的某边是否被照到。若vis[p1][p2]!=vis[p2][p1]则说明它是分界线。

　　3)三位面积计算：两个向量作三维叉积后将模长除2即可。

 

4.精度问题：

　　精度是计几永恒不变的话题。

　　考虑四点共面的情况，在上述做法中，加入其中三个点组成的平面后，第四个点会因为找不到这个平面而被忽略，事实上第四个点可能会增加这个面的面积。

　　为了避免这种情况，我们将每个点都作一些微小的“扰动”，这样就几乎不可能有四点共面的情况。同时，这个扰动幅度不能过大，不能影响到输出要求的精度。

　　但是同时，由于这种扰动，如果输入数据中有多个相同的点，在扰动幅度设的不好的情况下，会因为精度误差使所有坐标相同的点全部被认为使不同的点，从而导致凸包面数指数型增长。

　　实测扰动范围在1e-8左右可以同时一定程度上有效避免这两个问题，但一定也能被卡掉。也就是说网上大部分代码是可以轻松被卡掉的。具体应该怎么做才能避免精度问题感觉十分困难。

 #include<cmath>
 #include<cstdio>
 #include<algorithm>
 #define rep(i,l,r) for (int i=(l); i<=(r); i++)
 using namespace std;

 const int N=;
 const double eps=1e-;
 double ans;
 int n,cnt,tot;
 bool vis[N][N];
 double rs() {return (rand()/(double)RAND_MAX-0.5)*eps;}

 struct P{ double x,y,z; }p[N];
 double len(P a){ return sqrt(a.x*a.x+a.y*a.y+a.z*a.z); }
 void shake(P &a){ a.x+=rs(); a.y+=rs(); a.z+=rs(); }
 P operator -(const P &a,const P &b){ return (P){a.x-b.x,a.y-b.y,a.z-b.z}; }
 P operator *(const P &a,const P &b){ return (P){a.y*b.z-a.z*b.y,a.z*b.x-a.x*b.z,a.x*b.y-a.y*b.x}; }
 double mul(const P &a,const P &b){ return a.x*b.x+a.y*b.y+a.z*b.z; }

 struct F{ int v[]; }f[N],tmp[N];
 P Normal(F &a){ return (p[a.v[]]-p[a.v[]])*(p[a.v[]]-p[a.v[]]); }
 double area(F &a){ return len(Normal(a))/.; }
 bool see(F &a,P &b){ return mul(b-p[a.v[]],Normal(a))>; }

 void Convex(){
     f[++tot]=(F){,,}; f[++tot]=(F){,,};
     rep(i,,n){
         int tot1=;
         rep(j,,tot){
             bool fl=see(f[j],p[i]);
             if (!fl) tmp[++tot1]=f[j];
             rep(k,,) vis[f[j].v[k]][f[j].v[(k+)%]]=fl;
         }
         rep(j,,tot) rep(k,,){
             int x=f[j].v[k],y=f[j].v[(k+)%];
             if (vis[x][y] && !vis[y][x]) tmp[++tot1]=(F){x,y,i};
         }
         tot=tot1; rep(j,,tot1) f[j]=tmp[j];
     }
 }

 int main(){
     scanf("%d",&n);
     rep(i,,n) scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].z),shake(p[i]);
     Convex();
     rep(i,,tot) ans+=area(f[i]); printf("%.3lf\n",ans);
     return ;
 }