巧用 Python 找工作（资料在文末）

前言

近年来 Python 之火大家都有感而知，那亲们知道北京的 Python 开发岗位、运维开发岗位招聘地域都是如何分布的吗？薪水如何？是否有前景等等，这些数据呢直接通过招聘信息来了解到企业用人是最直接的，也是最简单的途径。

那本次将通过分享 Python 来抓取拉钩的招聘信息，然后加以分析，做一个北京的 Python 职位地域分布、薪资范围、福利待遇等维度出一个简单的分析报告，希望能帮助到想在 Python 这片田地耕耘的童鞋在发展方向上有所参考。

用到的工具

使用 Python 的 requests 工具到招聘网站爬取我们想要的数据，分析和可视化也使用 Python 的相关模块来实现，主要有如下：

Python 版本：Python 3.x

requests：发起请求，从网站抓取数据

math：数学运算函数，向上取整，这里主要用于分析数据

time：时间模块，主要是控制爬虫不会因为频繁请求而被网站拉进小黑屋

pandas：数据抓取后使用该模块保存为 csv 文件到本地

matplotlib：可视化画图

pylab：设置画图能显示中文

wordcloud、scipy、jieba（字符串分割成单词）：生成中文词云

如何进行数据抓取

使用 Chrome 打开拉钩网站，在网站输入“Python开发” 职位，使用 “检查” 功能查看网页源码。发现拉钩有反爬机制，职位信息并不在源代码里，而是在 JSON 文件里，因此直接通过 JSON 获取数据即可。

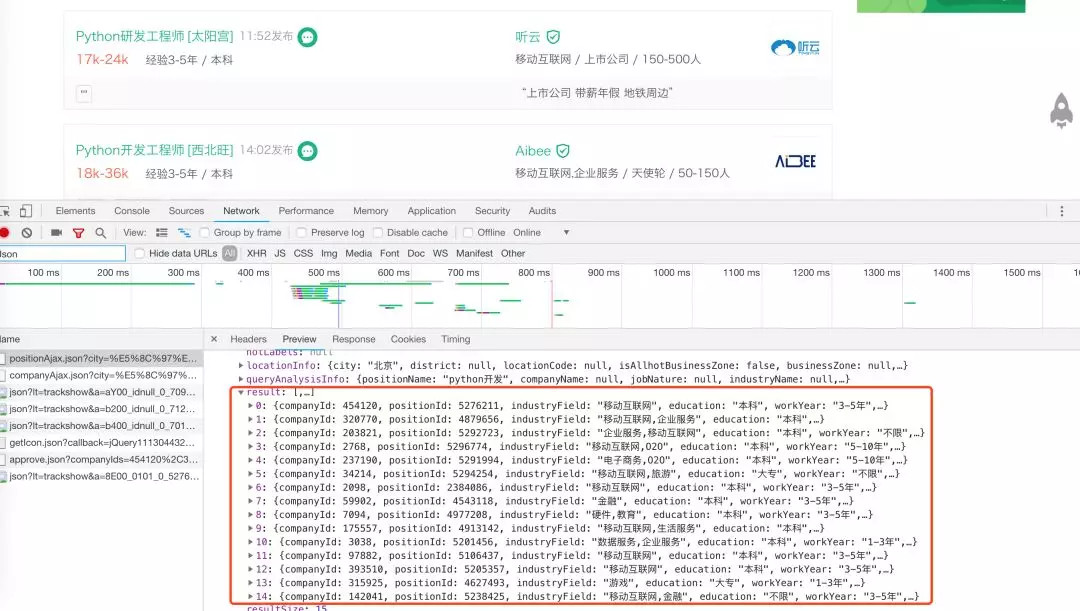
抓取信息时，需要加上头部信息，才能获取到数据。（原理很简单：你得伪装成一个正常的 client 去请求网页才能拿到想要的数据）

def get_json(url, num):
  '''从网页获取JSON,使用POST请求,加上头部信息'''
  headers = {
      'User-Agent': 'Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/66.0.3359.139 Safari/537.36',
      'Host': 'www.lagou.com',
 
    'Referer':'https://www.lagou.com/jobs/list_python%E5%BC%80%E5%8F%91?labelWords=&;fromSearch=true&suginput=',
      ',
    'X-Anit-Forge-Token': 'None',
    'X-Requested-With': 'XMLHttpRequest'
  }
 
  data = {
      'first': 'true',
      'pn': num,
      'kd': 'Python开发'}
  res = requests.post(url, headers=headers, data=data)
  res.raise_for_status()
  res.encoding = 'utf-8'
  # 得到包含职位信息的字典
  page = res.json()
  return page

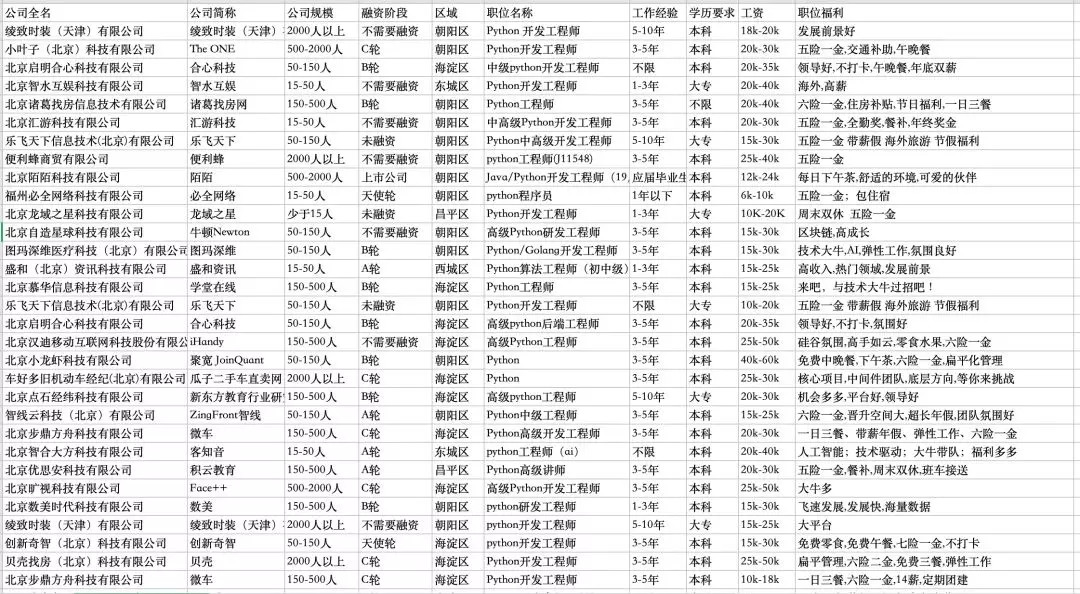
在搜索结果的第一页，我们可以从 JSON 里读取总职位数，按照每页 15 个职位，获得要爬取的页数。再使用循环按页爬取，将职位信息汇总，输出为 CSV格式。

序运行如下：

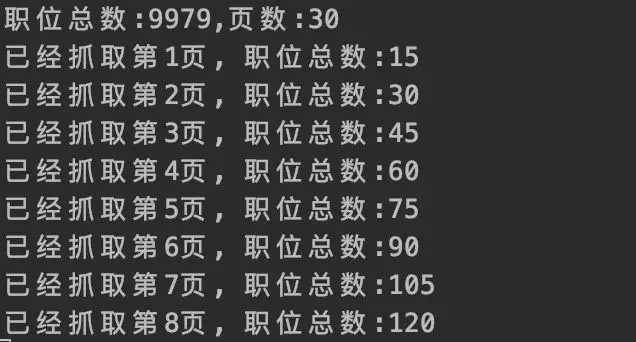
抓取结果如下：

数据可视化画图展示

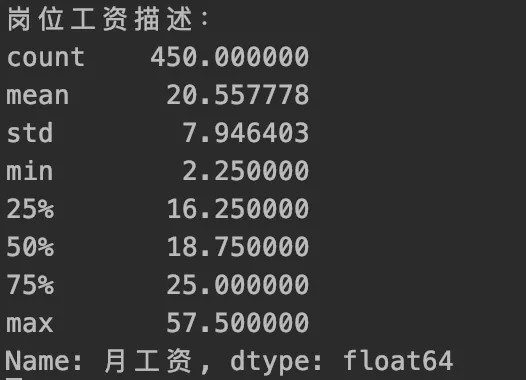
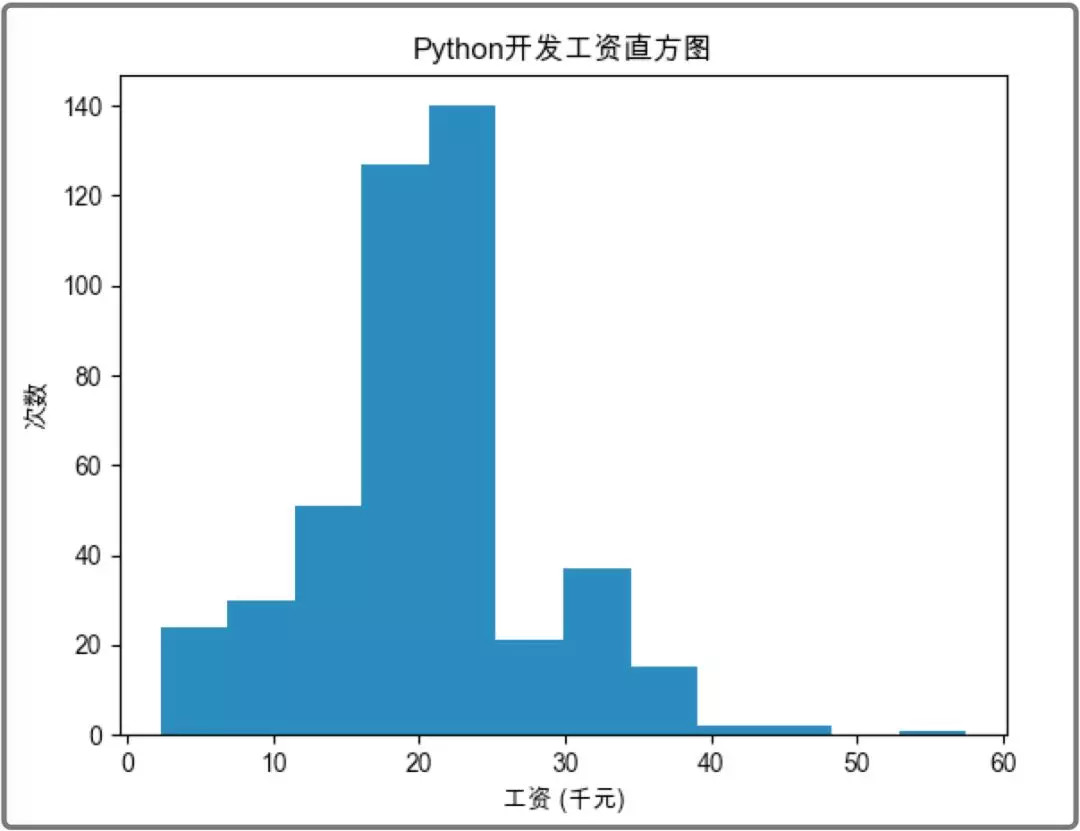
1、根据薪资制作直方图

薪资比例描述和可视化出图

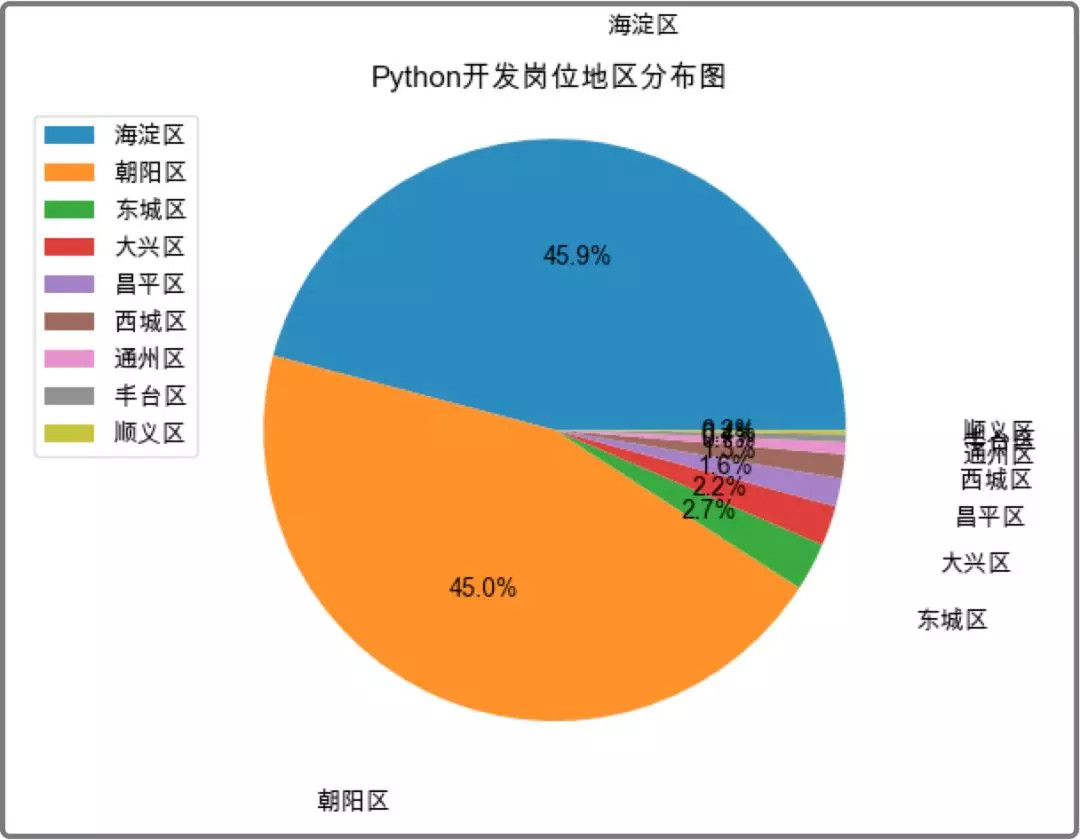
2、根据岗位地域分布制作饼图

3、制作词云

将职位福利这一列数据进行汇总，按照词语出现的频率生成云词实现 Python 可视化，以下是原图和云词图对比：

作者：Nick

某上市公司高级运维，业务运维负责人，主导运维自动化的开发与运维前沿技术的落地，曾就职中石油、魔秀科技，5年从业经验，经历了运维到运维开发的转变。

获取资料的方式如下：

Nick 分享<Python 分析拉钩职位>

时间：2018-11-15

21:00-22:00

PPT+ 视频

链接: https://pan.baidu.com/s/1tzG1adgpn23TSKvnR6XmYg 提取码: 2p2t

项目代码：https://github.com/nicksors/JobAnalysis

参与方式：扫码添加小助手备注：公开课，会拉入直播分享群分享结束后会把资料分享给大家