李航-统计学习方法-笔记-3：KNN

KNN算法

基本模型：给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例。这k个实例的多数属于某个类，就把输入实例分为这个类。

KNN没有显式的学习过程。

KNN使用的模型实际上对应于特征空间的划分。特征空间中，对每个训练实例点\(x_i\)，距离该点比其它点更近的所有点组成一个区域，叫作单元（cell）。每个训练实例拥有一个单元。所有的训练实例点的单元构成对特征空间的一个划分。如下图所示。

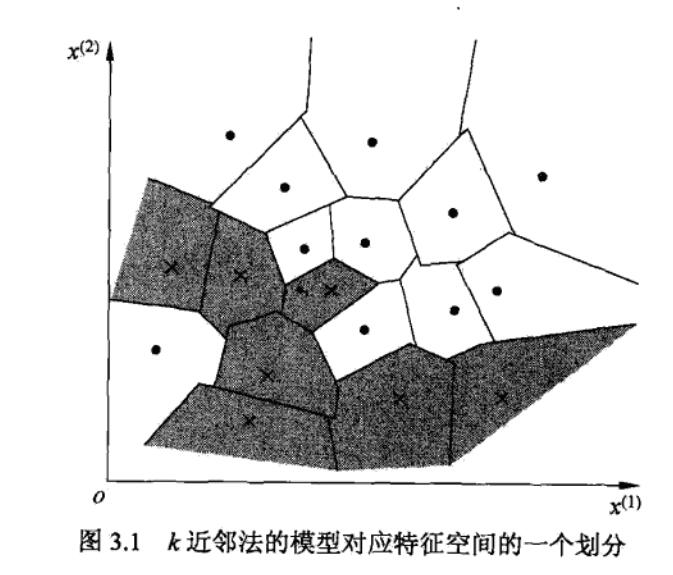
三要素：KNN模型由三个基本要素——距离度量，K值选择，分类决策决定。当三要素和训练集确定后，对任何一个新的输入实例，它所属的类唯一地确定。

KNN三要素之1——距离度量

由不同的距离度量所确定的最近邻点是不同的。

KNN的特征空间一般是n维实数向量空间\(R^n\)，使用的距离是欧氏距离。但也可以是其他距离，如更一般的\(L_p\)距离。设\(x_i\)为第\(i\)个样本，\(n\)维向量，\(x_i = (x_i^{(1)}, x_i^{(2)}, ..., x_i^{(n)})^T\)，则

\[L_p(x_i, x_j) = (\sum_{l=1}^{n} |\ x_i^{(l)} - x_j^{(l)}\ |^{\ p})^{\frac{1}{p}}, p \geqslant 1 \\
L_\infty(x_i, x_j) = \max_{l} |x_i^{(l)} - x_j^{(l)}|\]

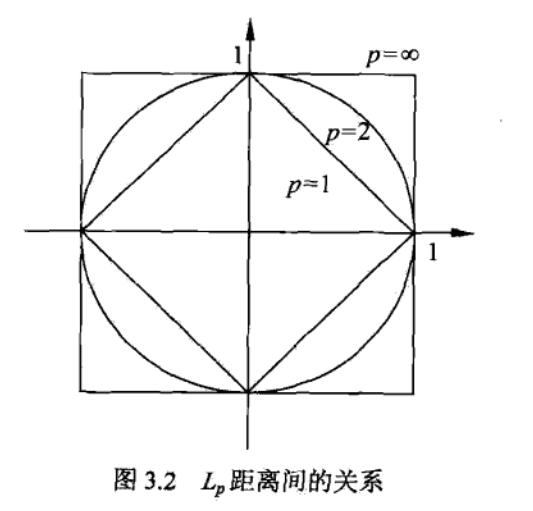
\(p=2\)时称为欧式距离，\(p=1\)称为曼哈顿距离。下图是二维空间中，与原点的\(L_p\)距离为1的图形。

\(p=1\)时，\(|x| + |y| = 1\)
\(p=2\)时，\(x^2 + y^2 = 1\)
\(p=\infty\)时，\(\max(|x|, |y|) = 1\)

KNN三要素之2——K值选择

K值的选择会对KNN结果产生重大影响

选择较小的K值：
如果选择较小的K值，相当于用较小的邻域中的训练实例进行预测，只有与输入实例较近的训练实例才会对预测结果起作用。“学习”的近似误差会减小。

缺点是“学习”的估计误差会增大，预测结果对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声，预测就会出错。

K值的减小意味着整体模型变得复杂，容易发生过拟合。

选择较大的K值：
如果选择较大的K值，相当于用较大邻域中的训练实例进行预测。其优点是减小学习的估计误差，缺点是近似误差会增大。这时离输入实例较远的训练实例起预测作用，使预测发生错误。

K值的增大意味着整体模型变得简单。K=N时，无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类，这时模型过于简单，完全忽略训练实例中的大量有用信息，是不可取的。

在应用中：
K值一般取一个比较小的数值，通常采用交叉验证法来选取最优的K值。

KNN三要素之3——分类决策规则

KNN的分类决策规则往往是多数表决，即由输入实例的K个邻近的训练实例中的多数类决定输入实例的类。

KNN的实现：kd树

kd树：KNN最简单的实现方法是线性扫描。这时要计算输入实例与每一个训练实例的距离。当训练集很大时，计算非常耗时，这种方法是不可行的。

为了提高KNN搜索的效率，可以考虑使用特殊的结构存储训练数据，以减少计算距离的次数。具体方法很多，下面介绍其中的kd树方法。

构造kd树：kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是二叉树，表示对k维空间的一个划分。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，构成一系列的k维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。

通常，依次选择坐标轴对空间切分，选择训练实例点在选定坐标轴上的中位数为切分点，这样得到的kd树是平衡的。注意，平衡的kd树搜索时的效率未必是最优的。

算法3.2 （构造平衡kd树）

输入：k维空间数据集\(T = \{x_1, x_2, ..., x_N\}\)，其中\(x_i = (x_i^{(1)}, x_i^{(2)}, ..., x_i^{(k)})^T\)，\(i = 1, 2, ..., N\)；

输出：kd树

（1）开始：构造根结点，根结点对应于包含\(T\)的k维空间的超矩阵区域。

选择\(x^{(1)}\)为坐标轴，以\(T\)中所有实例的\(x^{(1)}\)坐标的中位数为切分点，将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴\(x^{(1)}\)垂直的超平面实现。

由根结点生成的深度为1的左右子结点：左结点对应坐标\(x^{(1)}\)小于切分点的子区域，右结点对应坐标\(x^{(1)}\)大于切分点的子区域。将落在切分超平面上的实例点保存在根结点。

（2）重复：对深度为\(j\)的结点，选择\(x^{(j)}\)为切分的坐标轴，\(l = j(mod \ k) + 1\)，以该结点的区域中所有实例的\(x^{(l)}\)坐标的中位数为切分点。

由该结点生成深度为\(j+1\)的左右子结点：左结点对应坐标\(x^{(l)}\)小于切分点的子区域，右结点对应坐标\(x^{(l)}\)大于切分点的子区域。将落在切分超平面上的实例点保存在该结点。

（3）直到两个子区域没有实例存在时停止，从而形成kd树的区域划分。

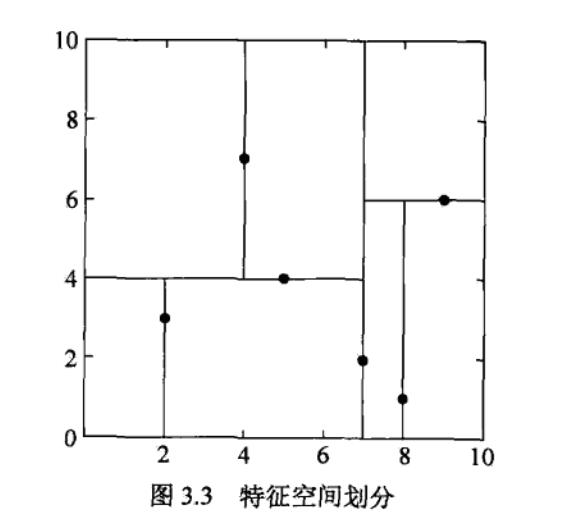
搜索kd树：利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。这里以最近邻为例加以叙述。

算法3.3 （用kd树的最近邻搜索）

输入：已构造的kd树；目标点x；
输出：x的最近邻

（1）从根结点出发，递归地向下访问kd树。若目标点x当前维的坐标小于切分点的坐标，则左移，否则右移，直到子结点为叶结点。
（2）以此叶结点为“当前最近点”。
（3）递归向上回退，在每个结点进行以下操作：

（a）若该结点保存的实例点比“当前最近点”离目标点更近，则以该实例点为“当前最近点”。

（b）检查另一子结点对应的区域是否与“以目标点为球心，以目标前与‘当前最近点’的距离为半径的超球体”相交。

如果相交，可能在另一子结点对应的区域内存在距离目标点更近的点，移动到另一结点，递归搜索。

如果不相交，向上回退。

（4）回退到根结点时，搜索结束。最后的“当前最近点”即为x的最近邻点。