洛谷P4170 [CQOI2007]涂色题解

废话：

这个题我第一眼看就是贪心呐， 可能是我之前那做过一道类似的题这俩题都是关于染色的

现在由于我帅气无比的学长的指导， 我已经豁然开朗， 这题贪心不对啊，

当时感觉自己好厉害贪心都能想出来

差点就觉得自己感动中国了

现在感觉自己仿佛是个zz

但是50分的话， 还是比较可观的(我在瞎说不要信

正文：

区间DP， 枚举区间 ，分为两个情况讨论

第一种情况：你现在枚举的这个区间[i, j]， 两边的颜色是一样的那么就从[i + 1. j]和[i, j - 1]里面选择较小的那一个

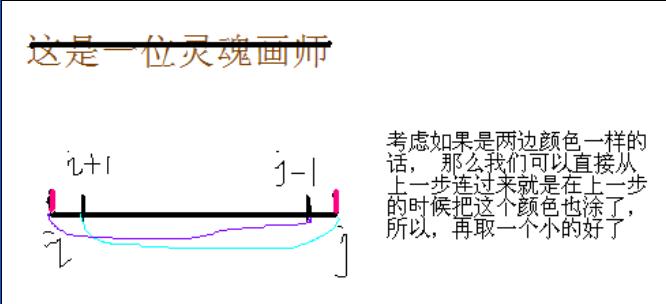
第二种情况：就是两边颜色不一样的情况， 直接枚举一个k合并区间即可

最后一定要注意：

f数组一定要初始化！

 memset (f, 0x3f3f3f, sizeof (f));
 for (int i = ; i <= len; i++)
   f[i][i] = ;

AC程序（我真的很喜欢自己的码风，等待挨喷）：

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = ;
char ch[N];
int f[N][N], len;
int main () {
    scanf ("%s", ch + );
    len = strlen (ch + );
    memset (f, 0x3f3f3f, sizeof (f));
    for (int i = ; i <= len; i++)
        f[i][i] = ;
    for (int l = ; l <= len; l++)
        for (int i = ; i + l -  <= len ; i++) {
            int j = i + l - ;
            if (ch[i] == ch[j])
                f[i][j] = min (f[i + ][j], f[i][j - ]);
            else for (int k = i; k < j; k++)
                f[i][j] = min (f[i][j], f[i][k] + f[k + ][j]);
        }
    printf ("%d\n", f[][len]);
    return ;
}

谢谢收看， 祝身体健康！