朴素贝叶斯算法源码分析及代码实战【python sklearn/spark ML】

一.简介　　
　　贝叶斯定理是关于随机事件A和事件B的条件概率的一个定理。通常在事件A发生的前提下事件B发生的概率，与在事件B发生的前提下事件A发生的概率是不一致的。然而，这两者之间有确定的
关系，贝叶斯定理就是这种关系的陈述。其中，L(A|B)表示在B发生的前提下，A发生的概率。L表示要取对数的意思。
　　关键词解释：
　　　　1.p(A),p(B)表示A，B发生的概率，也称先验概率或边缘概率。
　　　　2.p(B|A)表示在A发生的前提下，B发生的概率，也称后验概率。
　　基本公式：p(A|B) = p(AB)/p(B)
　　图解：

　　　　　　

　　备注：p(AB) = p(BA)都是指A,B同时发生的概率，所以可得贝叶斯公式：p(B|A) = p(AB)/p(A) = p(A|B)p(B)/p(A)导入数据得 = 0.5*0.4/0.8 = 0.25
　　贝叶斯公式：p(B|A) = p(A|B)p(B)/p(A)
　　图解：同上
　　朴素贝叶斯分类是一种十分简单的分类算法，其算法基础是对于给出的待分类项，求解在此项出现的条件下各类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。
　　实现步骤：

　　　　   　

二.代码实现【python】

 # -*- coding: utf- -*-
  """
  Created on Tue Oct  :: 

  @author: zhen
  """
  from sklearn.datasets import fetch_20newsgroups
  from sklearn.model_selection import train_test_split
  from sklearn.feature_extraction.text import CountVectorizer
 from sklearn.naive_bayes import MultinomialNB
 from sklearn.metrics import classification_report
 # 数据获取
 news = fetch_20newsgroups(subset='all')

 # 数据预处理:分割训练集和测试集
 x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25, random_state=)
 # 文本特征向量化
 vec = CountVectorizer()
 x_train = vec.fit_transform(x_train)
 x_test = vec.transform(x_test)

 # 使用朴素贝叶斯进行训练(多项式模型)
 mnb = MultinomialNB()
 mnb.fit(x_train, y_train)
 y_predict = mnb.predict(x_test)

 # 获取预测结果
 print(classification_report(y_test, y_predict, target_names = news.target_names))
 print("the accuracy of MultinomialNB is:", mnb.score(x_test, y_test))

三.结果【python】

　　

四.代码实现【Spark】

 package big.data.analyse.ml

 import org.apache.log4j.{Level,Logger}
 import org.apache.spark.NaiveBayes
 import org.apache.spark.ml.linalg.Vectors
 import org.apache.spark.ml.feature.LabeledPoint
 import org.apache.spark.sql.{SparkSession}

 /**
   * Created by zhen on 2019/9/9.
   */
 object NaiveBayesAnalyse {
   Logger.getLogger("org").setLevel(Level.WARN)
   def main(args: Array[String]) {
     val spark = SparkSession.builder().appName("NaiveBayes").master("local[2]").getOrCreate()

     /**
       * 加载数据
       */
     val test_data_array = Array("0,1.2-0.5-0.2","0,2.1-0.3-0.2","0,3.6-0.1-1.0","0,4.6-0.3-0.2",
           "1,0.4-1.5-0.2","1,0.2-2.6-0.8","1,0.6-3.3-0.6","1,0.1-4.3-0.4",
           "2,0.1-0.4-1.8","2,0.2-0.4-2.1","2,0.3-0.1-3.3","2,0.5-0.2-4.1")

     val sc = spark.sparkContext
     val test_data = sc.parallelize(test_data_array).map(row => {
       val array = row.split(",")
       LabeledPoint(array(0).toDouble,Vectors.dense(array(1).split("-").map(_.toDouble)))
     })

     /**
       * 拆分数据为训练数据和测试数据
       */
     val splits = test_data.randomSplit(Array(0.8, 0.2), seed = 11L)
     val train = splits(0)
     val test = splits(1)

     /**
       * 创建朴素贝叶斯模型并训练
       * 使用多项式模型
       */
     val model = NaiveBayes.train(train, lambda = 1.0, modelType = "multinomial")

     /**
       * 预测
       */
     val predict = test.map(row => (row.label, model.predict(row.features)))
     val predict_show = predict.take(20)
     val test_take = test.take(20)
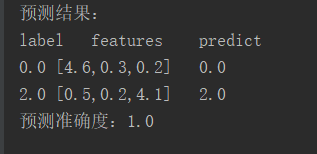
     println("预测结果：")
     println("label" + "\t" + "features" + "\t" + "predict")
     for(i <- 0 until predict_show.length){
       println(predict_show(i)._1 + "\t" + test_take(i).features +"\t" +  predict_show(i)._2)
     }

     val acc = 1.0 * predict.filter(row => row._1 == row._2).count() / test.count()
     println("预测准确度："+acc)
   }
 }

五.模拟源码实现【Spark】

NaiveBayes朴素贝叶斯类：

 package org.apache.spark

 import org.apache.spark.ml.feature.LabeledPoint
 import org.apache.spark.ml.linalg.{BLAS, DenseVector, SparseVector, Vector}
 import org.apache.spark.rdd.RDD

 /**
   * Created by zhen on 2019/9/11.
   */
 object NaiveBayes{
   /**
     * 多项式模型类别
     */
   val Multinomial : String = "multinomial"

   /**
     * 伯努利模式类型
     */
   val Bernoulli : String = "bernoulli"

   /**
     * 设置模型支持的类别
     */
   val supportedModelTypes = Set(Multinomial, Bernoulli)

   /**
     * 训练一个朴素贝叶斯模型
     * @param input 样本RDD
     * @return
     */
   def train(input : RDD[LabeledPoint]) : NaiveBayesModel = {
     new NaiveBayes().run(input)
   }

   /**
     * 训练一个朴素贝叶斯模型
     * @param input 样本RDD
     * @param lambda 平滑系数
     * @return
     */
   def train(input : RDD[LabeledPoint], lambda : Double) : NaiveBayesModel = {
     new NaiveBayes(lambda, Multinomial).run(input)
   }

   /**
     * 训练一个朴素贝叶斯模型
     * @param input 样本RDD
     * @param lambda 平滑系数
     * @param modelType 模型类型
     * @return
     */
   def train(input : RDD[LabeledPoint], lambda : Double, modelType : String) : NaiveBayesModel = {
     require(supportedModelTypes.contains(modelType), s"NaiveBayes was created with an unknown modelType:$modelType.")
     new NaiveBayes(lambda, modelType).run(input)
   }
 }

 /**
   * 贝叶斯分类类
   * @param lambda 平滑系数
   * @param modelType 模型类型
   */
 class NaiveBayes private(private var lambda : Double,
                          private var modelType : String) extends Serializable{

   import NaiveBayes.{Bernoulli, Multinomial}

   def this(lambda : Double) = this(lambda, NaiveBayes.Multinomial)

   def this() = this(1.0, NaiveBayes.Multinomial)

   /**
     * 设置平滑参数
     * @param lambda
     * @return
     */
   def setLambda(lambda : Double) : NaiveBayes = {
     this.lambda = lambda
     this
   }

   /**
     * 获取平滑参数
     * @return
     */
   def getLambda : Double = this.lambda

   /**
     * 设置模型类型
     * @param modelType
     * @return
     */
   def setModelType(modelType : String) : NaiveBayes = {
     require(NaiveBayes.supportedModelTypes.contains(modelType), s"NaiveBayes was created with an unknown modelType :$modelType.")
     this.modelType = modelType
     this
   }

   /**
     * 获取模型类型
     * @return
     */
   def getModelType : String  = this.modelType

   /**
     * 运行算法
     * @param data
     * @return
     */
   def run(data : RDD[LabeledPoint]) : NaiveBayesModel = {
     val requireNonnegativeValues : Vector => Unit = (v : Vector) => {
       val values = v match {
         case sv : SparseVector => sv.values
         case dv : DenseVector => dv.values
       }
       if(!values.forall(_ >= 0.0)){
         throw new SparkException(s"Naive Bayes requires nonnegative feature values but found $v.")
       }
     }

     val requireZeroOneBernoulliValues : Vector => Unit = (v : Vector) => {
       val values = v match{
         case sv : SparseVector => sv.values
         case dv : DenseVector => dv.values
       }
       if(!values.forall(v => v == 0.0 || v == 1.0)){
         throw new SparkException(s"Bernoulli naive Bayes requires 0 or 1 feature values but found $v.")
       }
     }

     /**
       * 对每个标签进行聚合操作，求得每个标签标签对应特征的频数
       * 以label为key，聚合同一个label的features，返回(label, (计数, features之和))
       */
     println("训练数据：")
     data.foreach(println)
     val aggregated = data.map(row => (row.label, row.features))
　　　　　　.combineByKey[(Long, DenseVector)](
       createCombiner = (v : Vector) => { //完成样本从v到c的转化：(v:Vector) -> (c:(Long, DenseVector))
         if(modelType == Bernoulli){
           requireZeroOneBernoulliValues(v)
         }else{
           requireNonnegativeValues(v)
         }
         (1L, v.copy.toDense)
       },
       mergeValue = (c : (Long, DenseVector), v : Vector) => { // 合并
         requireNonnegativeValues(v)
         BLAS.axpy(1.0, v, c._2)
         (c._1 + 1L, c._2)
       },
       mergeCombiners = (c1 : (Long, DenseVector), c2 : (Long, DenseVector)) => {
         BLAS.axpy(1.0, c2._2, c1._2)
         (c1._1 + c2._1, c1._2)
       }
     ).collect()

     val numLabels = aggregated.length // 类别标签数量

     var numDocuments = 0L // 文档数量
     aggregated.foreach{case (_, (n, _)) =>
       numDocuments += n
     }

     val numFeatures = aggregated.head match {case (_, (_, v)) => v.size} // 特征数量

     val labels = new Array[Double](numLabels) // 标签列表列表

     val pi = new Array[Double](numLabels) // pi类别的先验概率

     val theta = Array.fill(numLabels)(new Array[Double](numFeatures)) // theta各个特征在类别中的条件概率

     val piLogDenom = math.log(numDocuments + numLabels * lambda) //聚合计算theta

     var i = 0
     aggregated.foreach{case (label, (n, sumTermFreqs)) =>
       labels(i) = label
         pi(i) = math.log(n + lambda) - piLogDenom // 计算先验概率，并取log
       val thetaLogDenom = modelType match {
         case Multinomial => math.log(sumTermFreqs.values.sum + numFeatures * lambda) // 多项式模型
         case Bernoulli => math.log(n + 2.0 * lambda) // 伯努利模型
         case _ => throw new UnknownError(s"Invalid modeType: $modelType.")
       }
         var j = 0
         while(j < numFeatures){
           theta(i)(j) = math.log(sumTermFreqs(j) + lambda) - thetaLogDenom // 计算各个特征在各个类别中的条件概率
           j += 1
         }
         i+= 1
     }
     new NaiveBayesModel(labels, pi, theta, modelType)
   }
 }　　

NaiveBayesModel朴素贝叶斯模型类：

 package org.apache.spark

 import org.apache.spark.ml.linalg.{BLAS, Vector, DenseMatrix, DenseVector}
 import org.apache.spark.mllib.util.Saveable
 import org.apache.spark.rdd.RDD

 /**
   * Created by zhen on 2019/9/12.
   */
 class NaiveBayesModel private[spark](
                                       val labels : Array[Double],
                                       val pi : Array[Double],
                                       val theta : Array[Array[Double]],
                                       val modelType : String
                                     ) extends Serializable with Saveable{

   import NaiveBayes.{Bernoulli, Multinomial, supportedModelTypes}

   private val piVector = new DenseVector(pi) // 类别的先验概率

   private val thetaMatrix = new DenseMatrix(labels.length, theta(0).length, theta.flatten, true) // 各个特征在各个类别的条件概率

   private[spark] def this(labels:Array[Double], pi:Array[Double], theta:Array[Array[Double]]) = this(labels, pi, theta, NaiveBayes.Multinomial)

   /**
     * java接口的构造函数
     */
   private[spark] def this(
                            labels : Iterable[Double],
                            pi : Iterable[Double],
                            theta : Iterable[Iterable[Double]]
                          ) = this(labels.toArray, pi.toArray, theta.toArray.map(_.toArray))

   require(supportedModelTypes.contains(modelType), s"Invalid modelType $modelType.Supported modelTypes are $supportedModelTypes.")

   /**
     * 伯努利模型额外处理
     */
   private val (thetaMinusNegTheta, negThetaSum) = modelType match {
     case Multinomial => (None, None)
     case Bernoulli =>
       val negTheta = thetaMatrix.map(value => math.log(1.0 - math.exp(value)))
       val ones = new DenseVector(Array.fill(thetaMatrix.numCols){1.0})
       val thetaMinusNegTheta = thetaMatrix.map{value => value - math.log(1.0 - math.exp(value))}
       (Option(thetaMinusNegTheta), Option(negTheta.multiply(ones)))
     case _ => throw new UnknownError(s"Involid modelType: $modelType.")
   }

   /**
     * 对样本RDD进行预测
     */
   def predict(testData : RDD[Vector]) : RDD[Double] = {
     val bcModel = testData.context.broadcast(this)
     testData.mapPartitions{ iter =>
       val model = bcModel.value
       iter.map(model.predict) // 调用参数为一个样本的predict
     }
   }

   /**
     * 根据一个样本的特征向量进行预测
     */
   def predict(testData : Vector) : Double = {
     modelType match {
       case Multinomial =>
         val prob = thetaMatrix.multiply(testData)
         RBLAS.axpy(1.0, piVector, prob)
         labels(prob.argmax)
       case Bernoulli =>
         testData.foreachActive{(index, value) =>
           if(value != 0.0 && value != 1.0){
             throw new SparkException(s"Bernouslli naive Bayes requires 0 or 1 feature values but found $testData.")
           }
         }
         val prob = thetaMinusNegTheta.get.multiply(testData)
         BLAS.axpy(1.0, piVector, prob)
         BLAS.axpy(1.0, negThetaSum.get, prob)
         labels(prob.argmax)
       case _ =>
         throw new UnknownError(s"Involid modelType: $modelType.")
     }
   }

   /**
     * 保存模型
     */
   def save(sc : SparkContext, path : String) : Unit = {
     //val data = NaiveBayesModel.SaveLoadV2_0.Data(labels, pi, theta, modelType)
     //NaiveBayesModel.SaveLoadV2_0.save(sc, path, data)
   }

   override protected def formatVersion : String = "2.0"
 }

六.结果【Spark】