python 排序归并排序

算法思想

　　迭代法：

归并算法一共有两种思想，笼统的说，这两种思想的区别就在于一种不分割未排序的序列（直接将序列看为n个个数为1的子序列），这种称为---迭代法

直接从队头开始，两两合并为一个个数为2的子序列，一共有ceil(n/2)个，最后一个为2或者1，

接下来，以上面的结果开始，若序列个数不是1，将两个子序列合并为一个4个元素的子序列。完成后，得到ceil（n/4）个，元素可能为1，2，3，4个

重复上述过程

def merge_sort5(collection):

    length=len(collection)

    #定义合并数组函数，参数是两个数组，返回一个包含两个数组的结果集

    def merge(collection1,collection2):#数组长度可能不相等

        result=[]

        while collection1 and collection2:

        # while len(collection1)>=1 and len(collection2)>=1:#不要这样写

            result.pop(collection1.pop(0) if collection1[0]<=collection2[0] else collection2.pop(0))

            # result.append(collection1.pop(0)) if collection1[0]<=collection2[0] else result.append(collection2.pop(0))

        return result+collection1+collection2#比下面的好

        # result.extend(collection1+collection2)

        # return result

    temps=[pow(2,i) for i in range(15)]

    #定义存放根据步长切分后多余的,当有多余的让他和前面多余的进行合并

    superfluous=[]

    for temp in temps:

        flage=True

        left_index=-1

        while left_index+2*temp<length:#减一是因为截取的时候不到右边

            #这里可能会出错哦

            flage=False

            collection[left_index+1:left_index+2*temp+1]=merge(collection[left_index+1:left_index+temp+1],collection[left_index+temp+1:left_index+2*temp+1])

            left_index+=2*temp

        superfluous=merge(superfluous,collection[left_index+1:])#将多余的放到这里，当有新的多余的和老的合并

        del(collection[left_index+1:])

        if flage:

            break

    return superfluous

　　算法分析：稳定排序，需要O(n)额外空间、时间复杂度（一共有log（2，N）次外循环，内层循环分别为（n/1,n/2,n/4....n/temp)而（每次内循环中的归并操作的时间复杂度都是temp，）所有内层循环的时间复杂度是N（即n/temp*temp)所以T(n)=nlog(2,n),根据换地公式，log(2,n)=log(1,n)/log(1,2),考虑到取同数量级时不考虑系数，所以T(n)=O(nlogn)

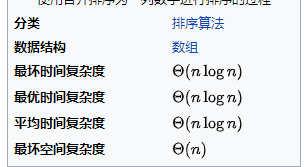
比较

　　仍然没有快排快：随机数据时间是快排的两倍

(sort) λ python some_sort.py

详细数据：[0.00100016594, 0.00299906731, 0.00100016594, 0.00299859047, 0.00100040436, 0.00299811363, 0.00199818611, 0.00199770927, 0.00200009346, 0.00199866295, 0.00199770927, 0.00099945068, 0.00200

009346, 0.00099825859, 0.0019993782, 0.0030002594, 0.00099873543, 0.00199723244, 0.00100016594, 0.00199866295, 0.00199818611, 0.00099897385, 0.00299787521, 0.00100016594, 0.00199890137, 0.0009996891, 0.00199961662, 0.00099992752, 0.00199794769, 0.00099301338, 0.00299859047, 0.00099921227, 0.0019993782, 0.00099992752, 0.00199961662, 0.00199913979, 0.00100040436, 0.0019993782, 0.0009996891, 0.00199961662, 0.00199842453, 0.00099873543, 0.0029976368, 0.00100016594, 0.00299835205, 0.00099921227, 0.00299882889, 0.0009996891, 0.00299835205, 0.00200009346, 0.00199985504, 0.00299835205, 0.0009996891, 0.00199866295, 0.00199961662, 0.00299930573, 0.00099873543, 0.00199985504, 0.00301456451, 0.00099849701, 0.00299859047, 0.00099825859, 0.00200128555, 0.00199866295, 0.0009996891, 0.00199723244, 0.00199913979, 0.00199866295, 0.00100016594, 0.00199961662, 0.00099992752, 0.00199842453, 0.00099921227, 0.00199842453, 0.00099897385, 0.00199890137, 0.00199866295, 0.00199866295, 0.00099921227, 0.00199985504, 0.00099873543, 0.00199913979, 0.00099945068, 0.00199890137, 0.00299787521, 0.00199866295, 0.00199818611, 0.00099992752, 0.00199818611, 0.00099921227, 0.00199866295, 0.00099992752, 0.00199794769, 0.00100040436, 0.00299906731, 0.00099992752, 0.00199818611, 0.00099945068, 0.00199866295, 0.00099992752]

运行了100次，平均运行时间差(me-other)/(bubble-quick)(正数代表你是个弟弟）是：0.00176918983

前者(插入排序)平均运行时间0.00361800909,后者（快排）平均运行时间0.00184881926,前者约是后者的1.9569倍

　　比插入快一个数量级：

详细数据：[-0.02898788452, -0.02898383141, -0.02898526192, -0.02896666527, -0.02997136116, -0.02898812294, -0.02801847458, -0.02900123596, -0.02998185158, -0.02995634079, -0.02994823456, -0.02992892

265, -0.02899622917, -0.10892653465, -0.03997755051, -0.02798676491, -0.02946019173, -0.02899646759, -0.02998185158, -0.02795672417, -0.02894616127, -0.03098273277, -0.02894926071, -0.02896404266, -0.02900695801, -0.02801513672, -0.02901649475, -0.02798366547, -0.09094834328, -0.04997181892, -0.02819728851, -0.02898263931, -0.02879166603, -0.02898216248, -0.02898240089, -0.02900052071, -0.02798342705, -0.02898788452, -0.03598976135, -0.02799391747, -0.0279853344, -0.02898383141, -0.02896499634, -0.02799677849, -0.03098726273, -0.02698349953, -0.02898192406, -0.02800416946, -0.02898788452, -0.02897882462, -0.02699589729, -0.02898049355, -0.02898478508, -0.02797055244, -0.03001332283, -0.02898716927, -0.02798342705, -0.02899360657, -0.02898335457, -0.02797985077, -0.02797579765, -0.02797961235, -0.02798891068, -0.02898812294, -0.02796649933, -0.02997922897, -0.02796721458, -0.02697610855, -0.02898406982, -0.02798390388, -0.02801299095, -0.02999520302, -0.03098082542, -0.0290017128, -0.02898097038, -0.02995085716, -0.02899312973, -0.02798342705, -0.02799725533, -0.02898263931, -0.02898335457, -0.02794861794, -0.03400492668, -0.03496909142, -0.03293538094, -0.03296351433, -0.03296232224, -0.02998614311, -0.02898216248, -0.02798914909, -0.02898836136, -0.02896380424, -0.02897286415, -0.03096866608, -0.02999520302, -0.02998280525, -0.02898335457, -0.03000807762, -0.02799677849, -0.03100776672]

运行了100次，平均运行时间差(me-other)/(bubble-quick)(正数代表你是个弟弟）是：-0.03094664574

前者(归并迭代法排序)平均运行时间0.00373820066,后者（快排）平均运行时间0.03468484640,前者约是后者的0.1078倍

递归法

第二种思想：称为----------递归法，这种思想主要采用分治法，先分割，然后集成

分割：递归的将当前序列平均分成两半，直到分成1个1个的子序列（平均分成两半，也是有误差的，比如含有奇数个的序列就允许一个比另外一个多一个）

集成：在保持元素顺序的同时将上一步得到的子序列集成到一起

集成的详细步骤是：申请空间，长度为两个已经有序序列的和，用来存放合并后的数组

设置两个游标，均为两个序列的队头，比较两个序列，将小的一个放进结果集中，移位继续比较

当一个序列中的元素完了以后，将另一个序列中所剩下的元素全部放进结果集中

我的问题：递归法中第一步的分割有什么用呢？难道是控制分割的尺度？，不是，通过大致的分割和递归结合起来，能简化代码

def merge_sort6(collection):

    '''自己写的（递归法）'''

    #巧妙之处在于要想到能把merge和merge_sort6结合起来递归，思考的线索是根据参数的格式

    def merge(left,right):

        result=[]

        while left and right:

            result.append(left.pop(0) if left[0]<=right[0] else right.pop(0))

        return result+left+right

    #递归

    length=len(collection)

    if length==1:

        return collection

    while True:

        mid=length//2

        return(merge(merge_sort6(collection[:mid]),merge_sort6(collection[mid:])))

　　对比

　　与采用迭代法的相比，速度慢了一半，但胜在代码简单

详细数据：[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0009996891, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0

, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0009996891, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, -0.00099945068, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

运行了100次，平均运行时间差(me-other)/(bubble-quick)(正数代表你是个弟弟）是：0.00000999928

前者(归并迭代法排序)平均运行时间0.00001999378,后者（递归法）平均运行时间0.00000999451,前者约是后者的2.0005倍