matlab-双摆仿真

在物理学和数学中，在动力系统领域，双摆是一个摆锤，另一个摆锤连接在其末端，是一个简单的物理系统，具有丰富的动态特性，对初始条件具有很强的敏感性。双摆的运动由一组耦合的常微分方程控制并且是混沌的。

由于双摆运动涉及到二阶微分方程组，在matlab中对双摆的仿真需要用到ode45求其数值解。

（代码来自 https://wenku.baidu.com/view/f78cec060912a21615792925.html）

clear all;
%控制r1 r2两个角位移 就可改变双摆初状态
r1=0.8;
r2=0.8;
m1=1;
m2=1;
L1=1;
L2=1;
g=9.8;
Da=inline(['[x(3);x(4);',...
    'inv([(m1+m2)*L1,m2*L2*cos(x(1)-x(2));',...
    'm1*L1*cos(x(1)-x(2)),m1*L2])*'...
    '[m2*L2*x(4)^2*sin(x(2)-x(1))-(m1+m2)*g*sin(x(1));',...
    'm2*L1*x(3)^2*sin(x(1)-x(2))-m2*g*sin(x(2))]]'],'t','x',...
    'flag','m1','m2','L1','L2','g');
set(gcf,'DoubleBuffer','on');
[t,x]=ode45(Da,[0,20],[r1,r2,0,0],[],m1,m2,L1,L2,g);
axis([-(L1+L2),(L1+L2),-(L1+L2)*1.8,1]);
axis square;hold on;
gh1=plot([0,L1*exp(i*(x(1)-pi/2))],'r-');
set(gh1,'linewidth',2,'markersize',6,'marker','o');
gh2=plot([L1*exp(i*(x(1)-pi/2)),L1*exp(i*(x(1)-pi/2))+L2*exp(i*(x(2)-pi/2))],'b-');
set(gh2,'linewidth',2,'markersize',6,'marker','o');
for k=2:size(x,1);
    C1=[0,L1*exp(i*(x(k,1)-pi/2))];
    C2=[L1*exp(i*(x(k,1)-pi/2)),L1*exp(i*(x(k,1)-pi/2))+L2*exp(i*(x(k,2)-pi/2))];
    set(gh1,'xdata',real(C1),'ydata',imag(C1));
    set(gh2,'xdata',real(C2),'ydata',imag(C2));
    title(['t=',num2str(t(k))],'fontsize',12);
    pause(0.1);
end
% figure;
% subplot(2 ,3 ,1);plot(t,x(:,1));title('t-\theta_1');
% xlabel('t');ylabel('\theta_1');
% subplot(2 ,3 ,2);plot(t,x(:,2));title('t-\theta_2');
% xlabel('t');ylabel('\theta_2');
% subplot(2 ,3 ,3);plot(t,x(:,3));title('t-\omega_1');
% xlabel('t');ylabel('\omega_1');
% subplot(2,3,4);plot(t,x(:,4));title('t-\omega_2');
% xlabel('t');ylabel('\omega_2');
% subplot(2,3,5);plot(x(:,1),x(:,3));title('\theta_1-\omega_1');
% xlabel('\theta_1');ylabel('\omega_1');
% subplot(2,3,6);plot(x(:,2),x(:,4));title('\theta_2-\omega_2');

　　效果图和上图差不多，放一张截图

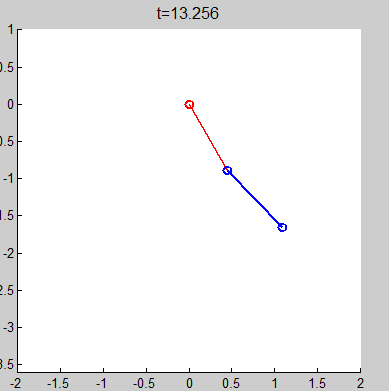
另外，科学网上也有对双摆的模拟程序

http://blog.sciencenet.cn/blog-292361-1038664.html