【机器学习】主成分分析法 PCA （II）

主成分分析法（PAC）的优化——选择主成分的数量

根据上一讲，我们知道协方差为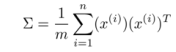①

而训练集的方差为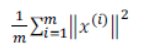②。

我们希望在方差尽可能小的情况下选择尽可能小的K值。

也就是说我们需要找到k值使得①/②的值尽可能小（≤0.01）

那么我们可以先令K = 1 然后进行主要成分分析，得到U reduce 和 Z 计算其比例是否小鱼0.01，如果不是就令K = 2 再进行计算。

直到找到使得比例满足的k的最小值。

不过，在octave中，我们也利用在调用svd函数时候，得到的 S，U ，V参数进行判断。S是一个n×n的对角矩阵，它的元素都在左对角线上。因此可以计算

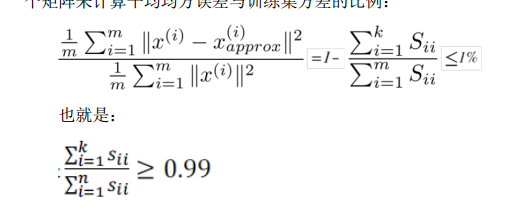
从而得到k的值。并且在压缩后，我们可以依据

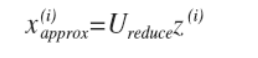
（其中 x approx ≈ x）来还原之前未被压缩的数据。

主成分分析法在机器学习过程中的应用：

例如，将100*100的图像压缩到1000个特征。

step 1）用PCA对特征值进行压缩

step 2）对训练集使用学习算法。

step 3）在预测时，采用学习得到的Ureduce将x特征转化成Z特征再进行预测。

使用时候可能存在的误区：

1）不要用PCA进行对过拟合的修正，此时可以尝试归一化。主要成分分析算法只是丢掉一些特征，不会考虑任何与结果有关的变量，这样做容易使对于本学习算法得重要的特征信息丢失。

2）降维不是所有机器学习算法的必要过程，因此不是所有的算法都要去使用，只是当算法运算太慢或者太消耗内存的时候，我们才会去考虑使用PCA算法进行优化。