Codeforces 781E Andryusha and Nervous Barriers 线段树 单调栈

原文链接https://www.cnblogs.com/zhouzhendong/p/CF781E.html

题目传送门 - CF781E

题意

　　有一个矩形，宽为 w ，高为 h 。一开始会有 w 个球分别从高处的每一个位置开始下落。

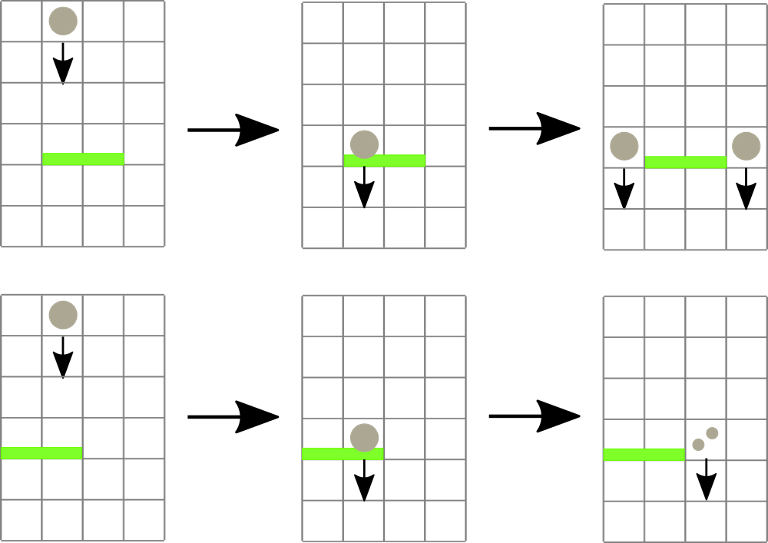
　　有 n 个挡板，每一个挡板有 4 个属性，分别是 u,L,R,s ，表示当前挡板的高度为 u ，横向覆盖的区间为 L,R ，如果球从高度大于 u+s 的地方开始下落到当前挡板，那么球会穿透当前挡板，否则球会分裂成两个，分别从该挡板的两边从新开始下落（如图的第一行），特殊地，当挡板的一段在边界上时，分裂得到的两个球都会从另一端下降（如图的第二行）。

　　问最终地面上能收到多少个球。

　　$w,n\leq 10^5,\ \ \  u,s,h\leq 10^9,\ \ 1\leq L\leq R\leq n$，保证每一行最多只有一个挡板，且不会有挡板两端都到达了边界。

　　　　

题解

　　首先，我们观察到如果直接 dp ，转移数就等于 挡板数×2+w （每一个挡板的两侧以及一开始投放的 w 个球）。

　　关键在于如何找到一个球从每一个位置开始下落会在哪里分裂。

　　我们来理一理思路：

　　我们要找的挡板要满足以下条件：

　　　　1.　高度小于当前高度。

　　　　2.　u+s 要大于等于当前高度。

　　　　3.　[L,R] 要包含当前横坐标。

　　　　4.　在满足上述条件的情况下，使得 u 最大。

　　显然可以发现可以树套树套树。但是这样显然不足以通过此题。

　　然后我们发现只需要把挡板按照高度从低到高排序，然后依次操作就好了，这样只需要树套树。但是这样的空间复杂度仍然是凉凉的。

　　于是，接下来是最重要的一步了！

　　一个挡板的纵向影响区间是 [u,u+s] ，对于这一维，我们可以直接用单调栈维护。

　　于是我们得到一个 线段树 + 单调栈的做法。可以通过本题。

　　时间复杂度 $O(n\log n)$ 。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL read(){
	LL x=0,f=1;
	char ch=getchar();
	while (!isdigit(ch)&&ch!='-')
		ch=getchar();
	if (ch=='-')
		f=-1,ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x*f;
}
const int N=100005,mod=1e9+7;
int n,h,w;
struct Node{
	int L,R,h,m,ans;
}a[N];
bool cmph(Node a,Node b){
	return a.h<b.h;
}
vector <int> s[N<<2];
void build(int rt,int L,int R){
	s[rt].push_back(1);
	if (L==R)
		return;
	int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
	build(ls,L,mid);
	build(rs,mid+1,R);
}
void Push(vector <int> &s,int x){
	while (a[s.back()].m<a[x].m)
		s.pop_back();
	s.push_back(x);
}
void update(int rt,int L,int R,int xL,int xR,int d){
	if (L>xR||R<xL)
		return;
	if (xL<=L&&R<=xR){
		Push(s[rt],d);
		return;
	}
	int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
	update(ls,L,mid,xL,xR,d);
	update(rs,mid+1,R,xL,xR,d);
}
int query(vector <int> &s,int h){
	while (a[s.back()].m<h)
		s.pop_back();
	return s.back();
}
int query(int rt,int L,int R,int x,int d){
	int ans=query(s[rt],d);
	if (L==R)
		return ans;
	int mid=(L+R)>>1,ls=rt<<1,rs=ls|1;
	if (x<=mid)
		return max(ans,query(ls,L,mid,x,d));
	else
		return max(ans,query(rs,mid+1,R,x,d));
}
int main(){
	h=read(),w=read(),n=read();
	for (int i=1;i<=n;i++){
		a[i].h=read(),a[i].L=read(),a[i].R=read();
		a[i].m=min(a[i].h+read(),(LL)h+1);
	}
	n++;
	a[n].h=0,a[n].L=1,a[n].R=w,a[n].m=1.05e9;
	sort(a+1,a+n+1,cmph);
	a[1].ans=1;
	for (int i=0;i<(N<<2);i++)
		s[i].clear();
	build(1,1,w);
	for (int i=2;i<=n;i++){
		if (a[i].L==1)
			a[i].ans=2*a[query(1,1,w,a[i].R+1,a[i].h)].ans%mod;
		else if (a[i].R==w)
			a[i].ans=2*a[query(1,1,w,a[i].L-1,a[i].h)].ans%mod;
		else
			a[i].ans=(a[query(1,1,w,a[i].L-1,a[i].h)].ans
					 +a[query(1,1,w,a[i].R+1,a[i].h)].ans)%mod;
		update(1,1,w,a[i].L,a[i].R,i);
	}
	int ans=0;
	for (int i=1;i<=w;i++)
		ans=(ans+a[query(1,1,w,i,h+1)].ans)%mod;
	printf("%d",ans);
	return 0;
}