Stanford机器学习---第一讲. Linear Regression with one variable

原文：http://blog.csdn.net/abcjennifer/article/details/7691571

本栏目（Machine learning）包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM（Support Vector Machines 支持向量机）、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。（https://class.coursera.org/ml/class/index）

第一章-------单参数线性回归 Linear Regression with one variable

(一)、Cost Function

线性回归是给出一系列点假设拟合直线为h(x)=theta0+theta1*x, 记Cost Function为J(theta0,theta1)

之所以说单参数是因为只有一个变量x，即影响回归参数θ1,θ0的是一维变量，或者说输入变量只有一维属性。

下图中为简化模式，只有theta1没有theta0的情况，即拟合直线为h(x)=theta1*x

左图为给定theta1时的直线和数据点×

右图为不同theta1下的cost function J(theta1)

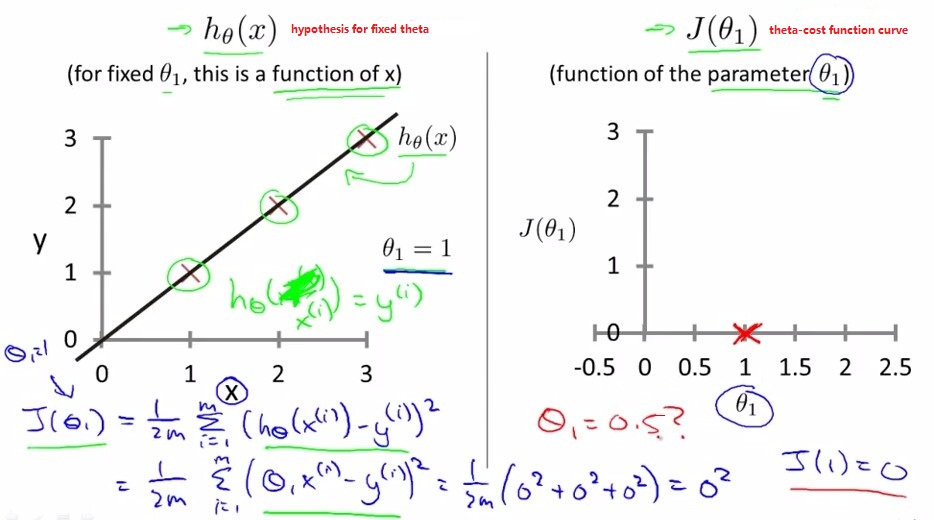
cost function plot:

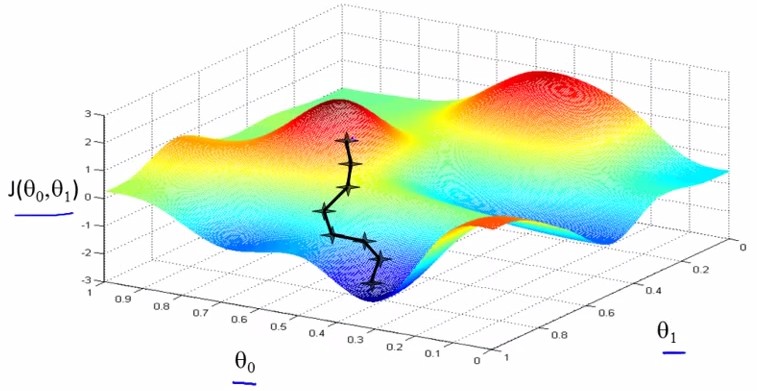
当存在两个参数theta0和theta1时，cost function是一个三维函数，这种样子的图像叫bowl-shape function

将上图中的cost function在二维上用不同颜色的等高线映射为如下右图，可得在左图中给定一个(theta0,theta1)时又图中显示的cost function.

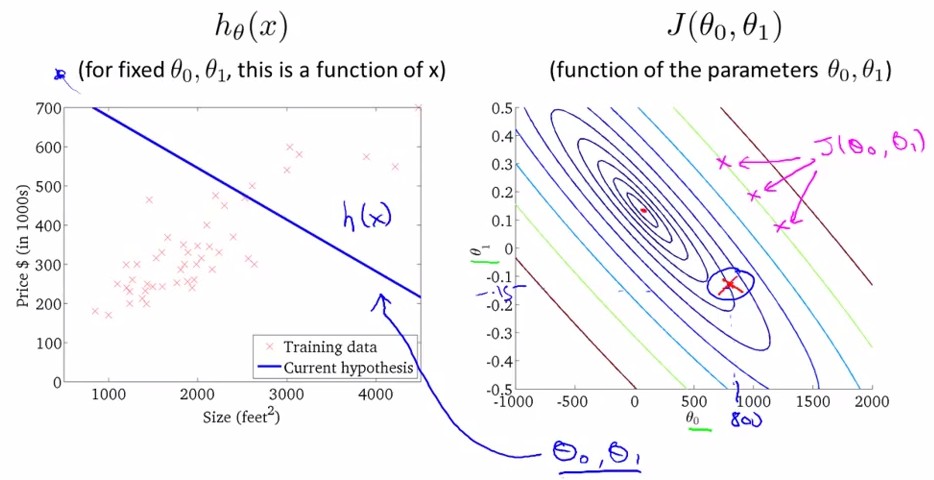
我们的目的是最小化cost function,即上图中最后一幅图，theta0=450,theta1=0.12的情况。

（二）、Gradient descent

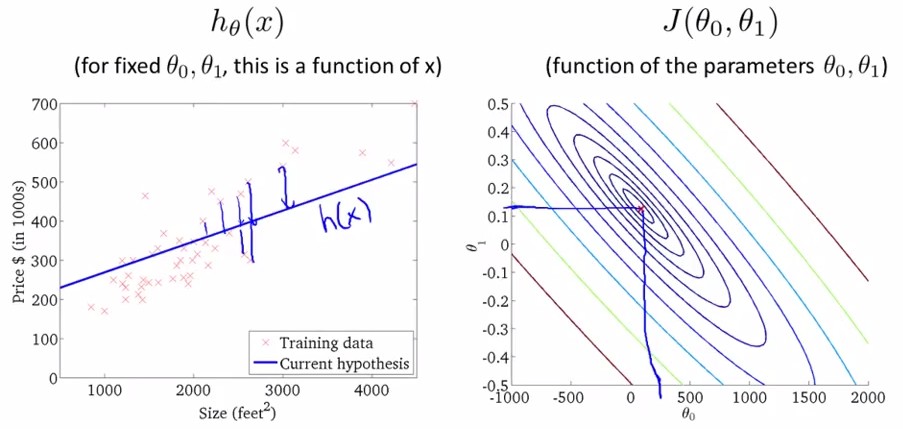
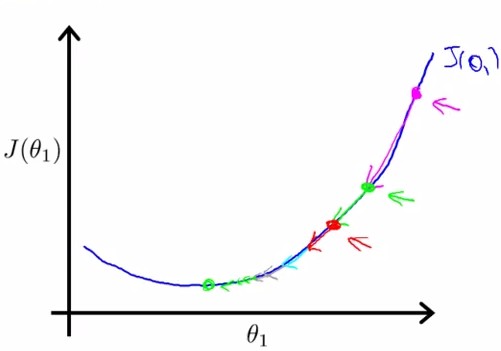
gradient descent是指梯度下降，为的是将cost funciton 描绘出之后，让参数沿着梯度下降的方向走，并迭代地不断减小J(theta0，theta1)，即稳态。

每次沿着梯度下降的方向：

参数的变换公式：其中标出了梯度（蓝框内）和学习率（α）：

gradient即J在该点的切线斜率slope，tanβ。下图所示分别为slope（gradient）为正和负的情况：

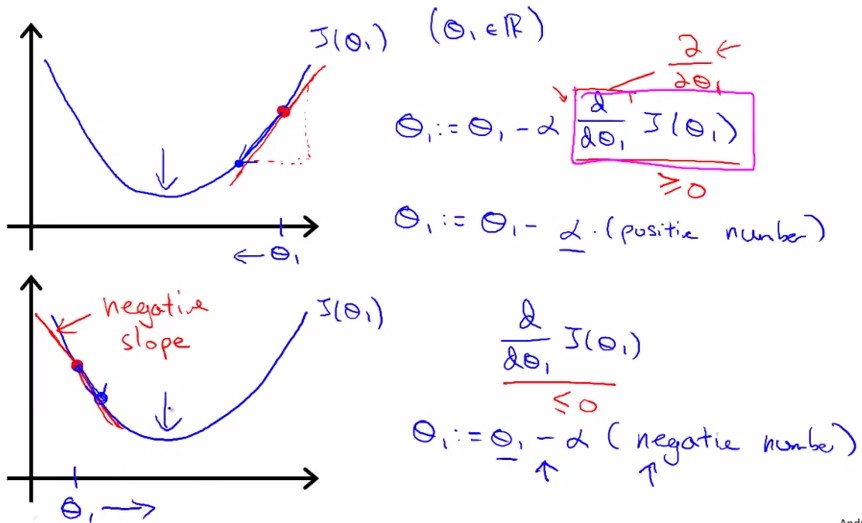
同时更新theta0和theta1，左边为正解：

关于学习率:

α太小：学习很慢；                                                             α太大：容易过学习

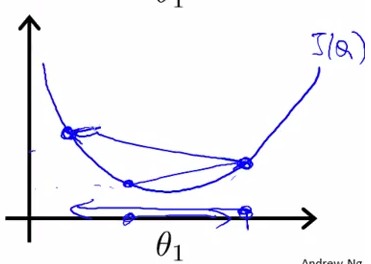
所以如果陷入局部极小，则slope=0，不会向左右变换

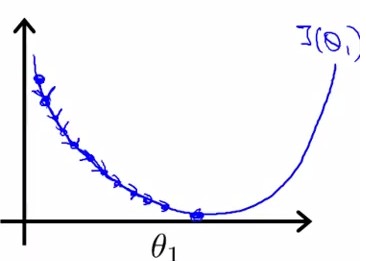
本图表示：无需逐渐减小α，就可以使下降幅度逐渐减小（因为梯度逐渐减小）：

求导后：

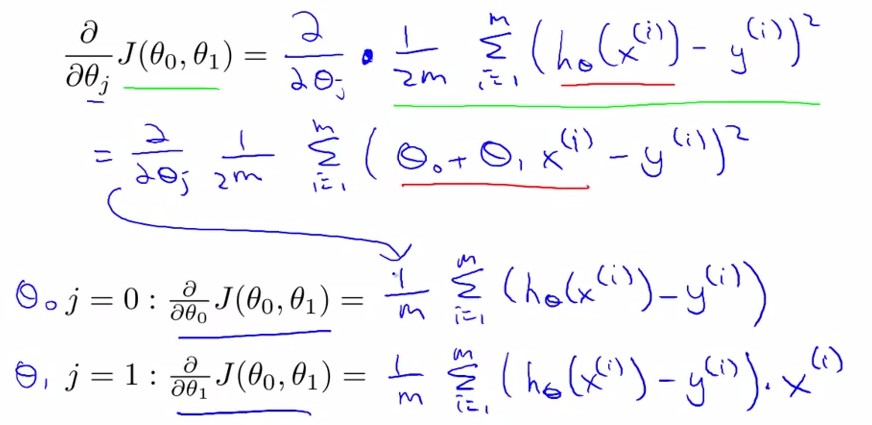
由此我们得到：

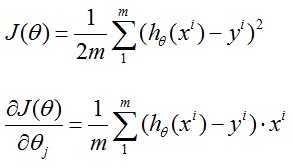
其中x(i)表示输入数据x中的第i组数据