KMP算法 --- 深入理解next数组

在KMP算法中有个数组，叫做前缀数组，也有的叫next数组。

每一个子串有一个固定的next数组，它记录着字符串匹配过程中失配情况下可以向前多跳几个字符。

当然它描述的也是子串的对称程度，程度越高，值越大，当然之前可能出现再匹配的机会就更大。

这个next数组的求法是KMP算法的关键，但不是很好理解。这个篇文章仅贡献给不喜欢看数学公式又想理解KMP算法的同学。

1、用一个例子来解释，下面是一个子串的next数组的值，可以看到这个子串的对称程度很高，所以next值都比较大。

位置i	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
前缀next[i]	0	0	0	0	1	2	3	1	2	3	4	5	6	7	4	0
子串	a	g	c	t	a	g	c	a	g	c	t	a	g	c	t	g

申明一下：下面说的对称不是中心对称，而是中心字符块对称，比如不是abccba，而是abcabc这种对称。

（1）逐个查找对称串

这个很简单，我们只要循环遍历这个子串，分别看前1个字符，前2个字符，3个... i个 最后到15个。

第1个a无对称，所以对称程度0

前两个ag无对称，所以也是0

依次类推前面0-4都一样是0

前5个agcta，可以看到这个串有一个a相等，所以对称程度为1前6个agctag，看得到ag和ag对成，对称程度为2

这里要注意了，想是这样想，编程怎么实现呢？

只要按照下面的规则：

a、当前面字符的前一个字符的对称程度为0的时候，只要将当前字符与子串第一个字符进行比较。这个很好理解，前面都是0，说明都不对称了，如果多加了一个字符，要对称的话最多是当前的和第一个对称。比如agcta这个里面t的是0，那么后面的a的对称程度只需要看它是不是等于第一个字符a了。

b、按照这个推理，我们就可以总结一个规律，不仅前面是0，如果前面一个字符的next值是1，那么我们就把当前字符与子串第二个字符进行比较，因为前面的是1，说明前面的字符已经和第一个相等了，如果这个又与第二个相等了，说明对称程度就是2了。有两个字符对称了。比如上面agctag，倒数第二个a的next是1，说明它和第一个a对称了，接着我们就把最后一个g与第二个g比较，又相等，自然对称成都就累加了，就是2了。

c、按照上面的推理，如果一直相等，就一直累加，可以一直推啊，推到这里应该一点难度都没有吧，如果你觉得有难度说明我写的太失败了。

当然不可能会那么顺利让我们一直对称下去，如果遇到下一个不相等了，那么说明不能继承前面的对称性了，这种情况只能说明没有那么多对称了，但是不能说明一点对称性都没有，所以遇到这种情况就要重新来考虑，这个也是难点所在。

（2）回头来找对称性

这里已经不能继承前面了，但是还是找对称成都嘛，最愚蠢的做法大不了写一个子函数，查找这个字符串的最大对称程度，怎么写方法很多吧，比如查找出所有的当前字符串，然后向前走，看是否一直相等，最后走到子串开头，当然这个是最蠢的，我们一般看到的KMP都是优化过的，因为这个串是有规律的。

在这里依然用上面表中一段来举个例子：

位置i=0到14如下,我加的括号只是用来说明问题：

(a g c t a g c )( a g c t a g c) t

我们可以看到这段，最后这个t之前的对称程度分别是：1，2，3，4，5，6，7,倒数第二个c往前看有7个字符对称，所以对称为7。但是到最后这个t就没有继承前面的对称程度next值，所以这个t的对称性就要重新来求。

这里首要要申明几个事实

1、t 如果要存在对称性，那么对称程度肯定比前面这个c 的对称程度小，所以要找个更小的对称，这个不用解释了吧，如果大那么t就继承前面的对称性了。

2、要找更小的对称，必然在对称内部还存在子对称，而且这个t必须紧接着在子对称之后。

如下图说明。

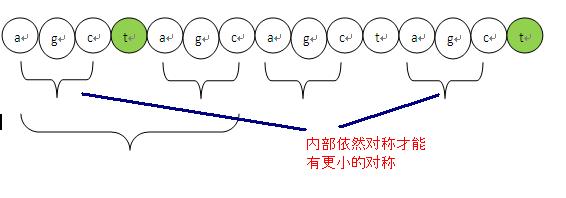
从上面的理论我们就能得到下面的前缀next数组的求解算法。

;
    ; )              
            ;
        ;       //如果遍历了所有子对称都无效，说明这个新字符不具有对称性，清0
    }
}

通过这个说明，估计能够理解KMP的next求法原理了。