hdu 4832 Chess(dp)

Chess

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 193    Accepted
Submission(s): 59

Problem Description

　　小度和小良最近又迷上了下棋。棋盘一共有N行M列，我们可以把左上角的格子定为(1,1)，右下角的格子定为(N,M)。在他们的规则中，“王”在棋盘上的走法遵循十字路线。也就是说，如果“王”当前在(x,y)点，小度在下一步可以移动到(x+1,
y), (x-1, y), (x, y+1), (x, y-1), (x+2, y), (x-2, y), (x, y+2), (x, y-2)
这八个点中的任意一个。

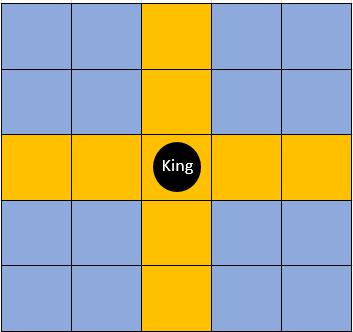
图1 黄色部分为棋子所控制的范围

　　小度觉得每次都是小良赢，没意思。为了难倒小良，他想出了这样一个问题：如果一开始“王”在(x₀,y₀)点，小良对“王”连续移动恰好K步，一共可以有多少种不同的移动方案？两种方案相同，当且仅当它们的K次移动全部都是一样的。也就是说，先向左再向右移动，和先向右再向左移动被认为是不同的方案。
　　小良被难倒了。你能写程序解决这个问题吗？

Input

输入包括多组数据。输入数据的第一行是一个整数T(T≤10)，表示测试数据的组数。
每组测试数据只包括一行，为五个整数N,M,K,x₀,y₀。(1≤N,M,K≤1000,1≤x₀≤N,1≤y₀≤M)

Output

对于第k组数据，第一行输出Case #k:，第二行输出所求的方案数。由于答案可能非常大，你只需要输出结果对9999991取模之后的值即可。

Sample Input

2
2 2 1 1 1
2 2 2 1 1

Sample Output

Case #1:
2
Case #2:
4

：：把二维转化成一维，因为对于x，y两者互不影响，只要求出对于x方向走i步sum1[i]，y方向走K-i步sum2[K-i];

那么就相当于在K个空格里放两样东西，个数分别为i,K-i;那么就有C[K][i]种情况

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 using namespace std;
 typedef long long ll;
 const int N = ;
 const int mod = ;
 int _,cas=,n,m;
 int dp[][N];
 int C[N][N],sum1[N],sum2[N];

 void calcu(int dp[][N],int sum[],int x,int step,int n)
 {
     int now = ;
     dp[now][x+] = ;
     sum[] =;
     for(int i = ; i <= step; i++)
     {
         now ^= ;
         sum[i] = ;
         for(int j = ; j <= n+; j++)//地图从下标2开始，免去一些判断
         {
             dp[now][j] = (dp[now^][j-] + dp[now^][j-] + dp[now^][j+] +dp[now^][j+]) % mod;
             sum[i] = (sum[i] + dp[now][j])%mod;
         }
     }
 }

 void solve()
 {
     int K,x0,y0;
     scanf("%d%d%d%d%d", &n, &m, &K, &x0, &y0);

     memset(dp,,sizeof(dp));
     calcu(dp,sum1,x0,K,n);
     memset(dp,,sizeof(dp));
     calcu(dp,sum2,y0,K,m);

     int ans = ;
     for(int i= ; i<=K; i++)
     {
         ans +=(ll)C[K][i] * sum1[i] %mod* sum2[K-i] % mod;
         ans %= mod;
     }
     printf("Case #%d:\n%d\n",cas++,ans);
 }

 void init()
 {
     C[][] =;
     for(int i = ; i <= ; i++)
     {
         C[i][] = C[i][i] = ;
         for(int j = ; j <= i; j++)
             C[i][j] = (C[i-][j] +C[i-][j-]) % mod;
     }
 }

 int main()
 {
 //    freopen("in.txt","r",stdin);
     init();
     scanf("%d", &_);
     while( _-- ) solve();
     return ;
 }