树上倍增求LCA及例题

先瞎扯几句

树上倍增的经典应用是求两个节点的LCA

当然它的作用不仅限于求LCA，还可以维护节点的很多信息

求LCA的方法除了倍增之外，还有树链剖分、离线tarjan ，这两种日后再讲（众人：其实是你不会吧:unamused:。。。）

思想

树上倍增嘛，顾名思义就是倍增

相信倍增大家都不默认，著名的rmq问题的$O(n*logn)$的解法就是利用倍增实现的

在树上倍增中，我们用

$f[j][i]$表示第$j$号节点，跳了$2^j$步所能到达的节点

$deep[i]$表示$i$号节点的深度

然后用这两个数组瞎搞搞就能整出LCA来啦

众人：:wrench: :hammer: :hocho:

实现

deep&&f[i][0]

首先，$f[i][0]$(也就是一个节点的上面的节点)容易求得，只要对整棵树进行一边dfs就好，在dfs的时候我们顺便可以求出$deep$数组

for(int i=head[now];i!=-;i=edge[i].nxt)

        if(!deep[edge[i].v])

            deep[edge[i].v]=deep[now]+,f[edge[i].v][]=now,dfs(edge[i].v);

这段代码应该不难理解

f[j][i]

那么我们怎么维护$f$数组呢？

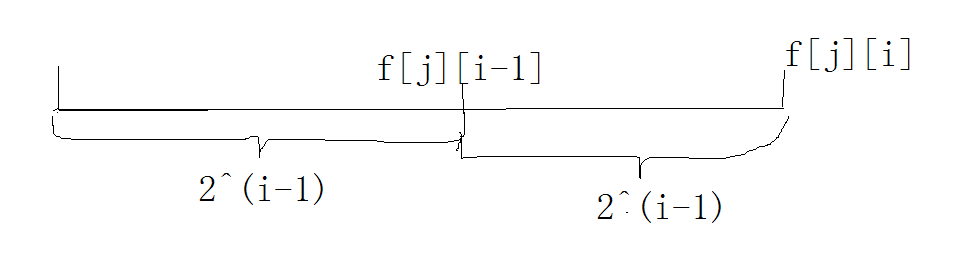
不难得到$f[j][i]=f[f[j][i-1]][i-1]$ 众人：难！

其实真的不难，一张图就可以解释明白啦

这句话的意思其实是说，一个节点跳$2^j$所能到达的节点实际上是跳$2^{i-1}$所能到达的节点再往上跳$2^{j-1}$步

注意$2^i=2^{i-1}+2^{i-1}$

代码：

for(int i=;i<=;i++)

    for(int j=;j<=n;j++)

        f[j][i]=f[f[j][i-]][i-];

LCA

接下来要进入最核心的部分啦，

我们如何用$deep$和$f$乱搞搞出$x$和$y$的LCA呢？

按照书上倍增算法的介绍

我们求LCA需要分为两步

设$deep[x]>deep[y]$

让$x$向上跳，跳到与$y$深度相同位置
让$x$和$y$同时向上跳，跳到祖先相同位置

根据二进制分解什么乱七八糟的，这么做一定是对的，其实这个挺显然的，yy一下就好了吧。。。

第一步

if(deep[x]<deep[y])    swap(x,y);

    for(int i=;i>=;i--)

        if(deep[f[x][i]]>=deep[y])

            x=f[x][i];

首先处理一下$x$和$y$的深度，保证$deep[x]>deep[y]$

然后尽量让$x$向上跳就好啦，注意这里是可以取到等号的

注意这里可能会出现一种特殊情况

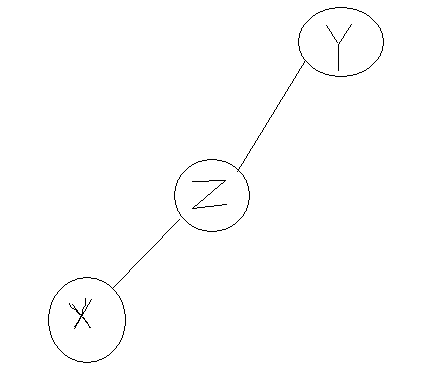
这个时候他们的最近公共祖先就是$y$

if(x==y)    return x;

第二步

同时向上跳，直到祖先相同为止

那么此时他们再向上跳一步所能到达的节点就是LCA啦

for(int i=;i>=;i--)

    if(f[x][i]!=f[y][i])

        x=f[x][i],y=f[y][i];

return    f[x][];

怎么样？

是不是很简单？

完整代码

#include<cstdio>

#include<cstring>

#include<algorithm>

using namespace std;

const int MAXN = ;

inline void read(int &n) {

    char c = getchar(); bool flag = ; n = ;

    while (c < '' || c > '')    c == '-' ? flag = , c = getchar() : c = getchar();

    while (c >= '' && c <= '')    n = n *  + c - , c = getchar(); flag ==  ? n = -n : n = n;

}

struct node {

    int v, nxt;

} edge[MAXN];

int head[MAXN];

int num = ;

inline void add_edge(int x, int y) {

    edge[num].v = y;

    edge[num].nxt = head[x];

    head[x] = num++;

}

int f[MAXN][];

int deep[MAXN];

int n, m, root;

void dfs(int now) {

    for (int i = head[now]; i != -; i = edge[i].nxt)

        if (!deep[edge[i].v])

            deep[edge[i].v] = deep[now] + , f[edge[i].v][] = now, dfs(edge[i].v);

}

void PRE() {

    for (int i = ; i <= ; i++)

        for (int j = ; j <= n; j++)

            f[j][i] = f[f[j][i - ]][i - ];

}

int LCA(int x, int y) {

    if (deep[x] < deep[y])    swap(x, y);

    for (int i = ; i >= ; i--)

        if (deep[f[x][i]] >= deep[y])

            x = f[x][i];

    if (x == y)    return x;

    for (int i = ; i >= ; i--)

        if (f[x][i] != f[y][i])

            x = f[x][i], y = f[y][i];

    return    f[x][];

}

int main() {

    memset(head, -, sizeof(head));

    read(n); read(m); read(root);

    for (int i = ; i <= n - ; i++) {

        int x, y; read(x); read(y);

        add_edge(x, y);

        add_edge(y, x);

    }

    deep[root] = ;

    dfs(root);

    PRE();

    for (int i = ; i <= m; i++) {

        int x, y;

        read(x); read(y);

        printf("%d\n", LCA(x, y));

    }

    return ;

}

例题

都是些入门难度的题目

洛谷P3379 【模板】最近公共祖先（LCA）

http://www.cnblogs.com/zwfymqz/p/6832524.html

POJ 1986 Distance Queries

http://www.cnblogs.com/zwfymqz/p/7791527.html

HDU 3078 Network

http://www.cnblogs.com/zwfymqz/p/7791617.html

HDU 2586 How far away ？

http://www.cnblogs.com/zwfymqz/p/7791517.html