vue中css样式不起作用，用！important也不起作用，此时需要用

/deep/

，没加之前是

加了之后起作用了，此时这个deep是深度作用域

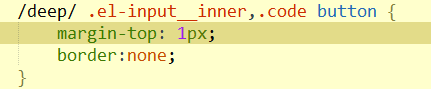
VUE中/deep/深度作用域的更多相关文章

  1. 深入理解 vue 中 scoped 样式作用域的规则

    哈喽!大家好!我是木瓜太香,今天我们来聊一个 vue 的样式作用域的问题,通常我们开发项目的时候是要在 style 上加上 scoped 来起到规定组件作用域的效果的,所以了解他们的规则也是很有必要的 ...

  2. vue中的css作用域、vue中的scoped坑点

    一.css作用域 之前一直很困扰css的作用域问题,即使是模块化编程下,在对应的模块的js中import css进来,这个css仍然是全局的.导致在css中需要加上对应模块的html的id/class ...

  3. vue中如何深度监听一个对象？

    大家都知道,Vue项目中对数据的监听,提供了一个很好的钩子watch,watch可以极其方便的监听我们常用数据类型值的变化,但通常当我们想监听一个对象中,某个属性值的变化时,很难达到我们预期的效果.那 ...

  4. vue中watch深度监听

    监听基本类型的都是浅度监听 watch的深度监听,监听复杂类型都是深度监听(funciton ,arrat ,object) // 监听对象 data(){ return { a:{ b:, c: } ...

  5. Deep learning for visual understanding: A review 视觉理解中的深度学习：回顾 之一

    Deep learning for visual understanding: A review 视觉理解中的深度学习:回顾 ABSTRACT: Deep learning algorithms ar ...

  6. vue中插槽作用域的使用

    一.插槽作用域 1.简单来说就是带参数的插槽: 2.使用方式: 在组件标签内部加一个template标签 在template标签上加一个属性scope 值随意书写 在组件内部用slot进行接受,如果给 ...

  7. Vue中的作用域插槽

    <!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title> ...

  8. 深度剖析Vue中父给子、子给父、兄弟之间传值！

    本片文章将为您详细讲解在Vue中,父给子传值.子给父传值以及兄弟之间传值方式! 父传子:父组件 // template里面 <aa :info="name"/> // ...

  9. 由 Vue 中三个常见问题引发的深度思考

    为什么 data 要写成函数,而不允许写成对象? Vue 中常说的数据劫持到底是什么? Vue 实例中数组改变 length 或下标直接赋值什么不能更新视图? http://www.sohu.com/ ...

随机推荐

  1. ABP中的Filter（上）

    这个部分我打算用上下两个部分来将整个结构来讲完,在我们读ABP中的代码之后我们一直有一个疑问?在ABP中为什么要定义Interceptor和Filter,甚至这两者之间我们都能找到一些对应关系,比如: ...

  2. codeforces16B

    Burglar and Matches CodeForces - 16B A burglar got into a matches warehouse and wants to steal as ma ...

  3. Ubuntu 16.04 RabbitMq 安装与运行（安装篇）

    Ubuntu 16.04 RabbitMq 安装与运行(安装篇) 2018年08月15日 15:05:24 我跟吴彦祖四六开 阅读数:1966   前言 目前公司用阿里云 + redis 的方式实现的 ...

  4. Flask 构建微电影视频网站(七)

    电影模块实现 上映预告 @home.route("/animation/") def animation(): """ 首页轮播动画 "&q ...

  5. SQL SERVER 查询所有数据表名称和数据行数

    SELECT a.name, b.rows FROM sysobjects AS a INNER JOIN sysindexes AS b ON a.id = b.id WHERE ( a.type ...

  6. Java基础 -- 持有对象(容器)

    一 容器的用途 如果对象的数量与生命周期都是固定的,自然我们也就不需要很复杂的数据结构. 我们可以通过创建引用来持有对象,如 Class clazz; 也可以通过数组来持有多个对象,如 Class[] ...

  7. Eclipse - 安装lombok后注解无效

    安装 lombok lombok 的安装过程挺简单的,网上已经有很多相关的博客,这里就不在多说了,可以参考这篇:eclipse集成lombok注解不起作用 但是我按照网上的方式安装之后,注解一直不起作 ...

  8. 开源顶级持久层框架——mybatis（ibatis）——day02

    mybatis第二天    高级映射 查询缓存 和spring整合          课程复习:         mybatis是什么?         mybatis是一个持久层框架,mybatis ...

  9. 轻型Database- sqlite入门

    SQLite 是一个软件库,实现了自给自足的.无服务器的.零配置的.事务性的 SQL 数据库引擎.SQLite 是在世界上最广泛部署的 SQL 数据库引擎.SQLite 源代码不受版权限制. 下面跟着 ...

  10. C语言数据类型和C#的区别