Jenkins结合.net平台综合应用之通过SSH方式拉取代码

上一节我们讲解了如何Jenkins如何通过轮训来监听git仓库变化然后拉取最新代码,上一节中我们使用的是https方式,然后正式环境中企业更倾向使用ssh方式.这里我们讲解一下如何通在Jenkins中配置ssh.

首先打开Jekins我们创建一个名为PullOverSSH的项目

在Source Code Management栏里,我们仍然选择git,这次仓库地址我们输入ssh地址

 

Credentials里我们点击后面的Add按钮.

出现如下对话框

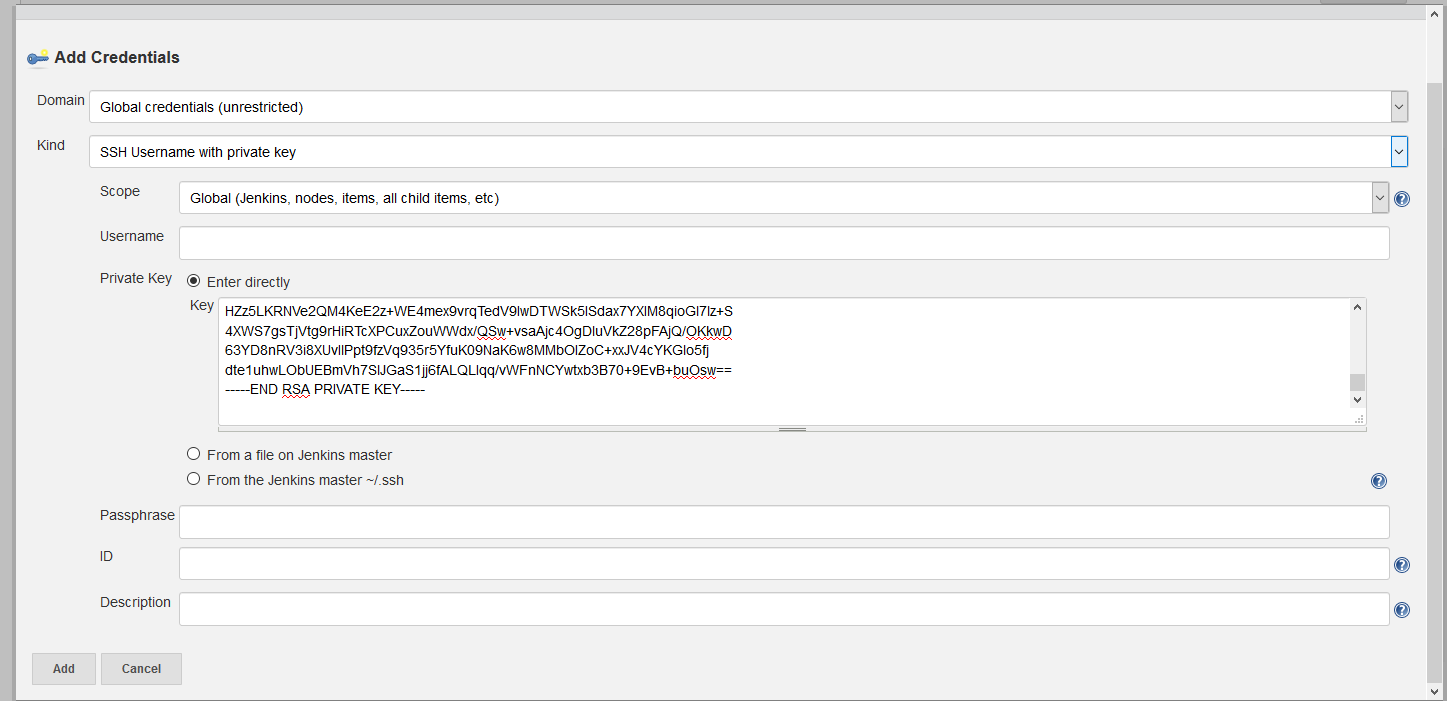
Kind下拉选择里选择如图示选项,private key我们选择enter directly,把密钥输入进去

关于如何生成私钥,公钥,以及如何使用请自行搜索查阅,这里不作介绍.

Passphrase为生成密钥时候的passhrase如果生成的时候我们一路回车,则此项不用填写,如果我们填写了passphrase,则这里需要填写生成时候的passphrase

然后点击add,这时候credential后面的下拉框里便可以看到我们刚添加的条目了

其中tylerzhou为刚添加的zypqqgc@qq.com为上节添加的,这里也解除有些读者的疑惑,是不是每次都要添加,答案是否定的,添加完成以后在新建其它项目里也会出现这些选项了,下次使用的时候就不需要添加了

然后再下面trigger栏目里配置如下

点击保存回到主界面

此时Jenkins会触发一次拉取,然后如果有更新则拉取最新,如果没有最新则不拉取.

我们查看一下上一节Pollscm项目的构建情况

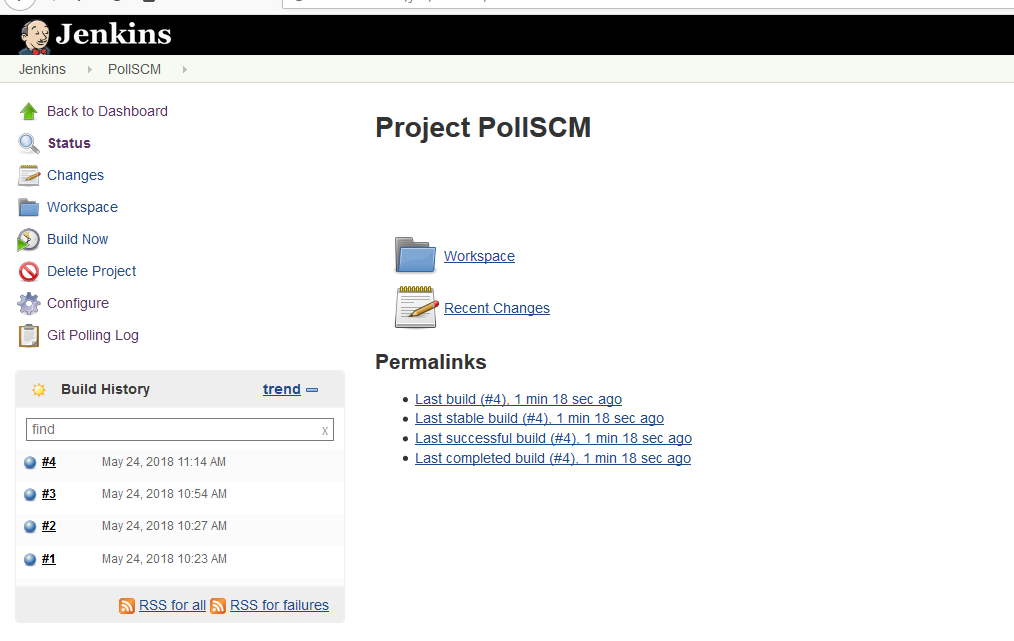
可以看到并不是每隔一分钟触发一次构建,而是有最新更新的时候才触发.