集成方法 Boosting原理

1.Boosting方法思路

Boosting方法通过将一系列的基本分类器组合，生成更好的强学习器

基本分类器是通过迭代生成的，每一轮的迭代，会使误分类点的权重增大

Boosting方法常用的算法是AdaBoost(Adaptive Boosting)、GBRT (Gradient Tree Boosting)

2.AdaBoost算法

算法要解决的2个问题（分类）

• 如何改变训练集的权值

　　提高前一轮分类错误样本的权值，降低分类正确样本的权值

• 如何将基本分类器组合成强学习器

　　加权多数表决法，通过投票来决定最后的结果，分类误差率小的基本分类器在投票中起较大作用，分类误差率大的基本分类器在投票中起较小作用。

算法思想

输入：训练集D；弱学习算法；训练轮数T

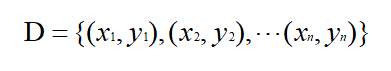
1）初始化权值分布D₁(x) = 1/n

2)(for i=1;i<T;i++){

　　a.计算不同基本分类器G的分类误差率e，找到最小分类误差率e_i；

　

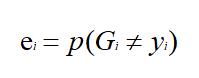
　　b.根据最小分类误差率e_i,选择最小的基本分类器G_i

　　c.计算G_i的权值α_i;

　　

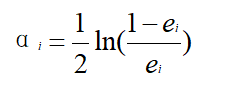
　　d.更新权值分布为D_i+1(x);

　

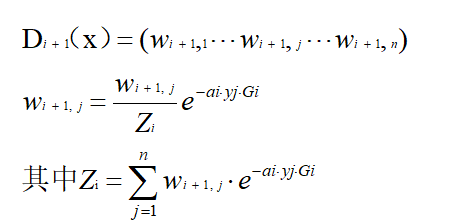
　　e.计算最终分类器G(x)，并用G(x)分类，没有误分类点退出循环

}

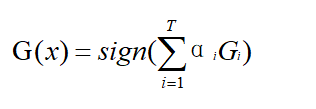
例子

例子来源于李航《统计学习方法》P140,数据表如下

x	0	1	2	3	4	5	6	7	8	9
y	1	1	1	-1	-1	-1	1	1	1	-1

首先是算法的输入，训练集D就是上边的表格，弱学习算法采用决策树桩（选一个数v,比v大的分一类，比v小的分一类），训练轮数输入5

1）初始化权值分布$D_1(x) =({1 \over 10}，{1 \over 10}，{1 \over 10}，{1 \over 10}，{1 \over 10}，{1 \over 10}，{1 \over 10}，{1 \over 10}，{1 \over 10}，{1 \over 10})$

2）第一轮，i=1

a.由于弱学习算法是决策树桩，v可取的值为0.5,1.5,2.5，…，8.5

case1:当x<v时，y=1;x>v时，y=-1;

当v取0.5时，x=1,2,6,7,8,9分错类，故e = ${0.1*1+0.1*1+0.1*1+0.1*1+0.1*1} = 0.5$

同理可求v取1.5,2.5，…，8.5时的分类误差率，不同v求得的分类误差率如下

0.5	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5
0.5	0.4	0.3	0.4	0.5	0.6	0.5	0.4	0.3

当v=2.5时，x=6,7,8分错类，分类误差率最低为e₁ = ${0.1*1+0.1*1+0.1*1} = 0.3$

case2:当x<v时，y=-1;x>v时，y=1;不同v求得的分类误差率如下

0.5	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5
0.5	0.6	0.7	0.6	0.5	0.4	0.5	0.6	0.7

b.因此可以得到基本分类器

$$G_1(x) = \begin{cases}1,&x<2.5\\-1,&x>2.5\end{cases}$$

c.计算G₁(x)的权值α₁

$$α_1 = {1 \over 2} ln {1- e_1 \over e_1} = 0.4236$$

d.更新权值分布为D₂(x)
$$Z_1=0.1*e^{-0.4236*1*1}+0.1*e^{-0.4236*1*1}+...+0.1*e^{-0.4236*-1*-1}=0.7e^{-0.4236}+0.3e^{0.4236}$$

$$w_{21}={0.1e^{-0.4236} \over 0.7e^{-0.4236}+0.3e^{0.4236}} = 0.07143$$

同理可以计算其他w_2j，最后得到更新后的权值分布D₂,这个D₂留着在下一轮用

$$D_2=(0.07143，0.07143，0.07143，0.07143，0.07143，0.07143，0.16667，0.16667，0.16667，0.07143)$$

e.计算第一轮最终分类器G(x)

$$G(x) =0.4236G_1(x) $$

用sign[G(x)]分类有x=6,7,8三个误分类点

第二轮，i=2

a.由于弱学习算法是决策树桩，v可取的值为0.5,1.5,2.5，…，8.5

case1:当x<v时，y=1;x>v时，y=-1;

0.5	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5
0.643	0.571	0.5	0.571	0.643	0.714	0.548	0.381	0.214

当v=8.5时，x=4,5,6分错类，分类误差率最低为e₂ = ${0.07143*1+0.07143*1+0.07143*1} =0.2143$

case2:当x<v时，y=-1;x>v时，y=1;不同v求得的分类误差率如下

0.5	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5
0.357	0.429	0.5	0.429	0.357	0.286	0.452	0.619	0.786

b.因此可以得到基本分类器

$$G_2(x) = \begin{cases}1,&x<8.5\\-1,&x>8.5\end{cases}$$

c.计算G₂(x)的权值α₂

$$α_2 = {1 \over 2} ln {1- e_2 \over e_2} = 0.6496$$

d.更新权值分布为D₃(x)

$$D_3=(0.0455，0.0455，0.0455，0.1667，0.1667，0.1667，0.1060，0.1060，0.1060，0.0455)$$

e.计算第二轮最终分类器G(x)

$$G(x) =0.4236G_1(x) + 0.6496G_2(x)$$

用sign[G(x)]分类有x=3,4,5三个误分类点

第三轮，i=3

a.由于弱学习算法是决策树桩，v可取的值为0.5,1.5,2.5，…，8.5

case1:当x<v时，y=1;x>v时，y=-1;

0.5	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5
0.409	0.364	0.318	0.485	0.652	0.818	0.712	0.606	0.5

case2:当x<v时，y=-1;x>v时，y=1;不同v求得的分类误差率如下

0.5	1.5	2.5	3.5	4.5	5.5	6.5	7.5	8.5
0.591	0.636	0.682	0.515	0.348	0.182	0.288	0.394	0.5

当v=5.5时，x=0,1,2,9分错类，分类误差率最低为e₃ = ${0.0455*1+0.0455*1+0.0455*+0.0455*1} =0.182$

b.因此可以得到基本分类器

$$G_3(x) = \begin{cases}-1,&x<5.5\\1,&x>5.5\end{cases}$$

c.计算G₃(x)的权值α₃

$$α_3 = {1 \over 2} ln {1- e_3 \over e_3} = 0.7514$$

d.更新权值分布为D₄(x)

$$D_4=(0.125,0.125,0.125,0.102,0.102,0.102,0.065,0.065,0.065,0.125)$$

e.计算第三轮最终分类器G(x)

$$G(x) =0.4236G_1(x) + 0.6496G_2(x)+0.7514G_3(x)$$

用sign[G(x)]分类有0个误分类点，故最终的分类器是

$$G(x) =0.4236G_1(x) + 0.6496G_2(x)+0.7514G_3(x)$$