PSO：利用PSO+ω参数实现对一元函数y = sin(10*pi*x) ./ x进行求解优化，找到最优个体适应度—Jason niu

x = 1:0.01:2;
y = sin(10*pi*x) ./ x;
figure
plot(x, y)
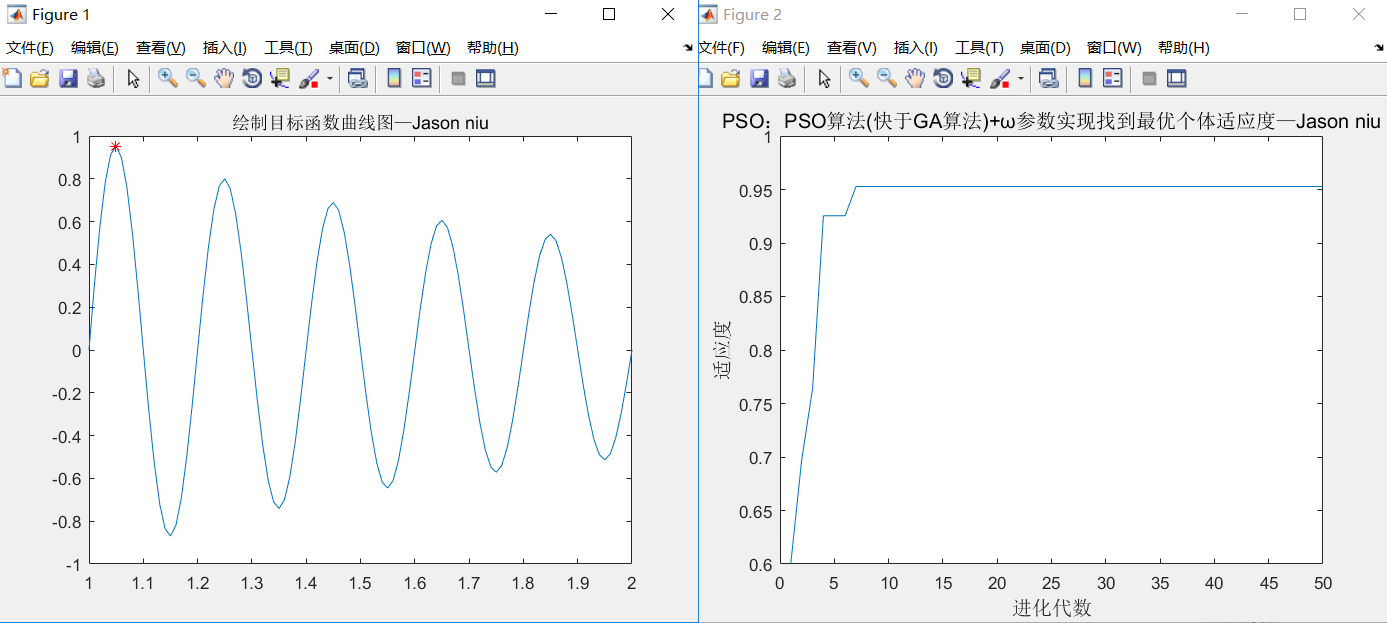
title('绘制目标函数曲线图—Jason niu');
hold on

c1 = 1.49445;
c2 = 1.49445;

maxgen = 50;
sizepop = 10;   

Vmax = 0.5;
Vmin = -0.5;
popmax = 2;
popmin = 1;

ws = 0.9;
we = 0.4;

for i = 1:sizepop

    pop(i,:) = (rands(1) + 1) / 2 + 1;
    V(i,:) = 0.5 * rands(1);  

    fitness(i) = fun(pop(i,:));
end

[bestfitness bestindex] = max(fitness);
zbest = pop(bestindex,:);
gbest = pop;
fitnessgbest = fitness;
fitnesszbest = bestfitness;   

for i = 1:maxgen
    w = ws - (ws-we)*(i/maxgen);
    for j = 1:sizepop

        V(j,:) = w*V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax)) = Vmax;
        V(j,find(V(j,:)<Vmin)) = Vmin;

        pop(j,:) = pop(j,:) + V(j,:);
        pop(j,find(pop(j,:)>popmax)) = popmax;
        pop(j,find(pop(j,:)<popmin)) = popmin;

        fitness(j) = fun(pop(j,:));
    end

    for j = 1:sizepop
        if fitness(j) > fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end

        if fitness(j) > fitnesszbest
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
    end
    yy(i) = fitnesszbest;
end

[fitnesszbest zbest]
plot(zbest, fitnesszbest,'r*')

figure
plot(yy)
title('PSO：PSO算法(快于GA算法)+ω参数实现找到最优个体适应度—Jason niu','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);