R语言-主成分分析

1.PCA

使用场景:主成分分析是一种数据降维,可以将大量的相关变量转换成一组很少的不相关的变量,这些无关变量称为主成分

　　步骤:

1. 数据预处理(保证数据中没有缺失值)
2. 选择因子模型(判断是PCA还是EFA)
3. 判断要选择的主成分/因子数目
4. 选择主成分
5. 旋转主成分
6. 解释结果
7. 计算主成分或因子的得分

　 案例:从USJudgeRatings数据集中有11个变量,如何去减化数据(单个主成分分析)

　　　　1.使用碎石图确定需要提取的主成分个数

 library(psych)
 # 1.做出碎石图确定主成分的个数
 fa.parallel(USJudgeRatings[,-1],fa='pc',n.iter = 100,show.legend = F,main = 'Scree plot with parallel analysis')

　　结论:在特征值大于1的的点附近,都表明保留1个主成分即可

　　2.提取主成分

 # 1.第一个参数是关系矩阵
 # 2.nfactors指定主成分的个数
 # 3.rotate指定旋转方法,默认varimax
 # 4.scores表示是否需要计算主成分得分,默认不需要
 pc <- principal(USJudgeRatings[,-1],nfactors = 1)
 pc

　　结论:第一主成分与每一个变量高度相关

　　3.获取主成分得分

 pc <- principal(USJudgeRatings[,-1],nfactors = 1,scores = T)
 head(pc$scores)
 cor(USJudgeRatings$CONT,pc$scores)

　　4.获取相关系数

 cor(USJudgeRatings$CONT,pc$scores)

　　结论:律师和法官的私交和律师的评级没有关系

　　案例2:减少女孩身体指标的主成分分析(多个主成分分析)

　　1.判断个数

 fa.parallel(Harman23.cor$cov,n.obs = 203,fa='pc',n.iter = 100,show.legend = F,
             main = 'Scree plot with parallel analysis')

　　结论:有2个点在水平线1上,所以需要2个主成分

　　2.主成分分析

pc2 <- principal(Harman23.cor$cov,nfactors = 2,rotate = 'none')
pc2

　　

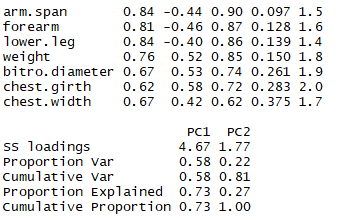
　　结论:需要对数据旋转作进一步分析

　　3.主成分旋转(尽可能对成分去噪)

 rc <- principal(Harman23.cor$cov,nfactors = 2,rotate = 'varimax')
 rc

　　4.获取主成分的得分系数

 round(unclass(rc$weights),2)

　　

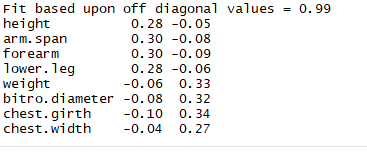
　　结论:可以通过系数*数值来计算出主成分得分

2.EFA

使用场景:探索因子分析发掘数据下一组较少的,无法观测的变量来解释一组可观测变量的相关性

　　案例:使用EFA对6个心理学测试来检测参与者的得分

　　1.判断需要提取的因子数

 covariances <- ability.cov$cov
 correlations <- cov2cor(covariances)
 fa.parallel(correlations,n.obs = 112,fa='both',n.iter=100,main = 'Scree plots with parallel analysis')

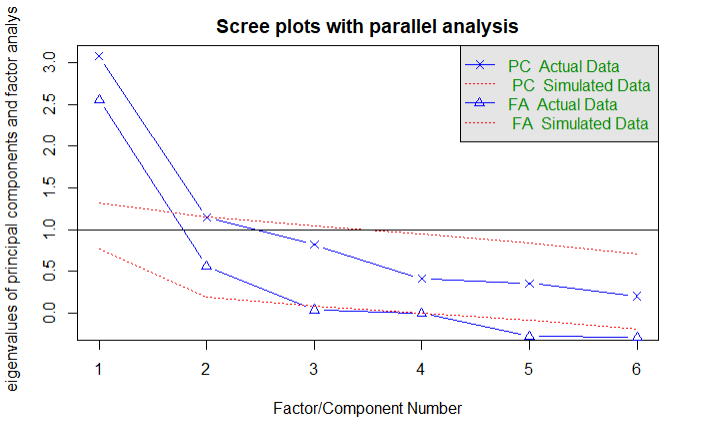
　　结论:需要提取2个因子,因为图形在拐点之上有2个分布

　　2.提取公共因子

 fa <- fa(correlations,nfactors = 2,rotate = 'none',fm='pa')
 fa

　　结论:2个因子解释了6个心理学测试的60%方差,需要进一步旋转

 fa.varimax <- fa(correlations,nfactors=2,rotate='varimax',fm='pa')
 fa.varimax

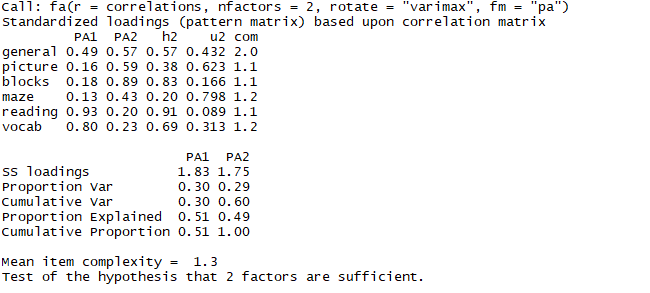
　　结论:阅读和词汇在第一个因子占比较大,画图,积木在第二个因子上成分较大,如果想进一步判断这个各因子是否相关,需要使用斜交旋转提取因子

 fa.promax <- fa(correlations,nfactors=2,rotate='Promax',fm='pa')
 fa.promax

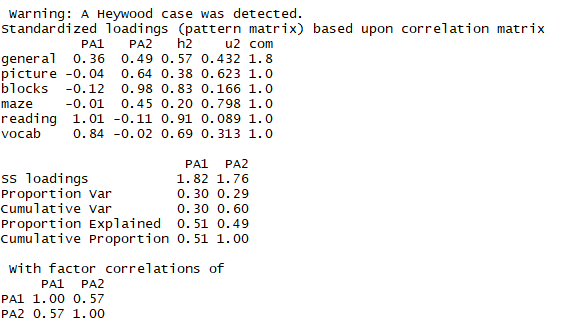
　　结论:相关性为0.57,相关性很大,如果相关性不大,使用正交旋转即可

　　3.计算得分

 fsm <- function(oblique) {
   if (class(oblique)[2]=="fa" & is.null(oblique$Phi)) {
     warning("Object doesn't look like oblique EFA")
   } else {
     P <- unclass(oblique$loading)
     F <- P %*% oblique$Phi
     colnames(F) <- c("PA1", "PA2")
     return(F)
   }
 }

 fsm(fa.promax)

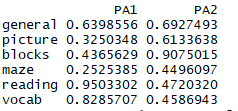
　　5.正交旋转所得因子得分图

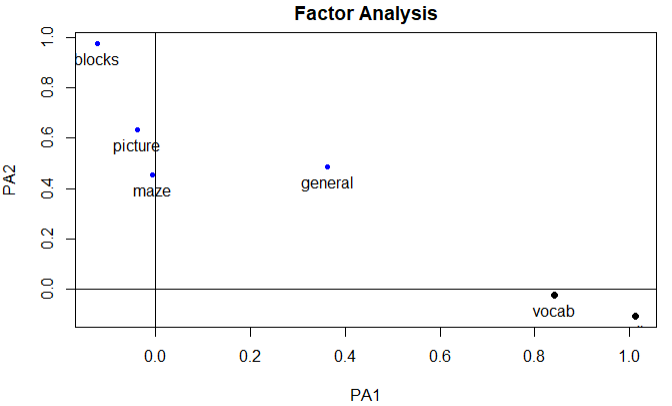
　　结论:词汇和阅读在第一因子上载荷较大,图片,迷宫,积木在第二个因子上载荷较大,普通智力检测在二者的分布较为平均

　　6.斜交旋转所生成的因子图

 fa.diagram(fa.promax,simple = F)

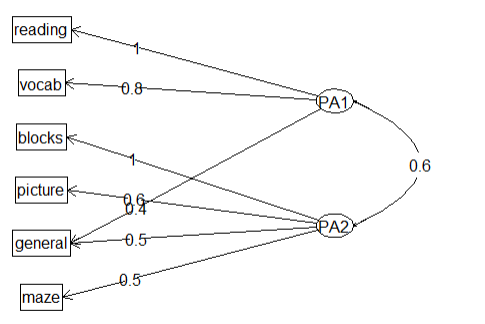
　　结论:显示了因子之间的关系,该图比上一张图更为准确