[BZOJ]1045 糖果传递(HAOI2008)

　　放一道数学题。

Description

　　有n个小朋友坐成一圈，每人有ai个糖果。每人只能给左右两人传递糖果。每人每次传递一个糖果代价为1。

Input

　　第一行一个正整数n<=1000000，表示小朋友的个数．接下来n行，每行一个整数ai，表示第i个小朋友得到的糖果的颗数。

Output

　　求使所有人获得均等糖果的最小代价。

Sample Input

　　4
　　1
　　2
　　5
　　4

Sample Output

　　4

HINT

　　n<=1000000，ai在int范围内。

Solution

　　这道题也算是一个经典的绝对值最值模型吧。（小C会说刚拿到这道题拿费用流跑二分图匹配？）

　　其实不要想着把一个地方的糖果搬到另一个地方去，我们要把题目化简：

　　整个过程都可以看作是一个小朋友向相邻的小朋友传递/接受糖果，

　　所以我们很自然地设pi为第i个小朋友向第i-1个（i+1亦可）小朋友传递的糖果数。pi可以为负（就变成了接收的糖果数）。

　　所以我们要使答案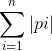最小。

　　重点来了！看到求绝对值之和最小的式子，根据我们的知识储备，我们推测它和中位数有关。

　　可是这里面有n个变量，我们要想办法把它化成只含一个变量的式子。我们开始推式子：

　　设ai的平均数为aver，我们有（显而易见的）n个等式：

　　　　  ······①

　　　　  ······②

　　　　……

　　　　

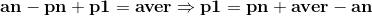
　　我们观察到，p2其实就是p1加上一个常数；而p3又是p2加上一个常数，所以p3就是p1加上一个常数！

　　同理p1~pn都可以用形如p1+d(d为常数)的式子来表示。

　　所以设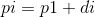，所以我们只要求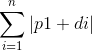的最小值！

　　这时候就可以用到我们的知识储备，p1只要取di的中位数的相反数就可以使答案最小！

#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define MN 1000005
using namespace std;
int n;
ll a[MN],b[MN],sum,lt,ans;

inline int read()
{
    int n=,f=; char c=getchar();
    while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
    while (c>='' && c<='') {n=n*+c-''; c=getchar();}
    return n*f;
}

int main()
{
    register int i;
    n=read();
    for (i=;i<=n;++i) sum+=a[i]=read();
    sum/=n;
    for (i=;i<n;++i) b[i+]=b[i]+sum-a[i];
    sort(b+,b+n+);
    lt=-b[n+>>];
    for (i=;i<=n;++i) ans+=abs(lt+b[i]);
    printf("%lld",ans);
}

Last Word

　　关于数学的最值问题，这种题型只是其中之一，小C以后见到了可能还会继续更新。