Kylin系列之二：原理介绍

Kylin系列之二：原理介绍

2018年4月15日

15:52

因何而生

Kylin和hive的区别

1. hive主要是离线分析平台，适用于已经有成熟的报表体系，每天只要定时运行即可。

2. Kylin主要是MLOAP（多维在线分析平台）。在线意味着提供快速的相应速度。主要适用于分析师不知道自己需要哪些数据，建立怎样的模型，需要不断的摸索，查询一致形成一个完整的模型和方案。

3. 通常的做法是在Kylin中进行数据的调研，探索，建立模型。形成固定模式后在hive中进行运行。

原理与架构

1. 基本原理是使用MR或者Spark对数据进行全方面的计算；然后将结果集存储到HBase中；分析师在进行数据调研时就可以直接访问HBase的结果集了。

2. 因为在Kylin进行预计算的过程中，我们是不知道分析师需要哪些结果的，因此，Kylin会尽可能多的尽心预计算，这样就会耗费很多的运算和存贮资源。因此如何对Cuboid进行修剪以及segmen的合并等是优化的重点

3. 如图我们可以看出Kylin的架构：

A. 预计算逻辑：通过REST API 或者JDBC，ODBC的方式，将Cube提交给Kylin引擎，引擎将Cube解析为相应的MR程序，从hive中获取数据相关的元素据，然后在Hadoop集群中运行，并将结果存储在HBase中。Cube预计算结束

B. 查询预计算逻辑：通过REST API 或者JDBC，ODBC的方式，将Cube提交给Kylin引擎，Kylin将数据解析为相应的HBase代码，在HBase中进行查询，然后将结果返回给调用方

4. Kylin在本质上只是一个查询解析引擎，将Cube或者SQL方言解析为相应的查询语句，然后脚本相应的服务端进行计算

A. Hive:主要提供表的元数据信息。Kylin链接Hive获取查询表在hdfs上的路径。

B. Hadoop:提供基础的数据存储服务。

C. MR/Spark:提供计算引擎，Kylin将Cube解析为相应的执行代码，交给MR/Spark运行。

D. HBase:负责存储Kylin中相关的Cube，Model元数据，并存放Cube进行预计算的结果集。

E. Zeppline/Tableau:进行结果数据的查询与展示。

架构如下（截图来自官网）：

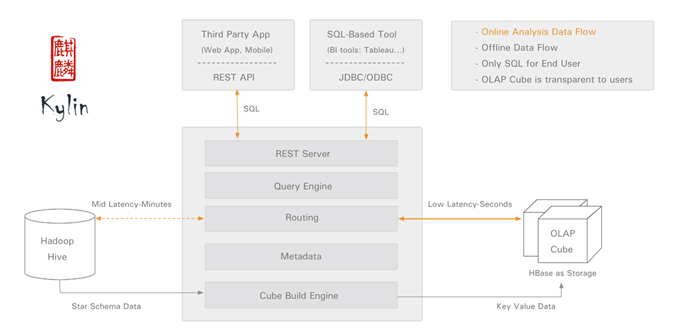
基本概念

维度（Dimension）和度量（Measure）

1. 维度是观察数据的角度，比如：人的性别，学生的年级等。在SQL中，我们可以认为被group by的字段就是维度。也可以理解为统计中的称名数据

2. 度量是表示可以用来计算的列，比如学生考试成绩，消费者的交易金额等。在SQL中我们可以认为可以被聚合函数进行计算，比如sum()，avg()的都是度量

3. 维度和度量并不是绝对意义的分割的，他们之间是可以相互转换的。比如我们要统计学生分数的分布情况，这个时候分数就是一个维度列；当我们统计学生的平均分时，这个时候分数就是一个度量列。

4. 维度的基数：即维度列字段的个数。如性别这一维度的基数是2，只有男女；季节这一维度列的基数是4，因为只有春夏秋冬四季。但是如果将学生的学号作为维度列的话，一个学校有1万名学生的话，该维度的基数列为1万。通产基数超过一百万的维度称为超高基数维度，需要引起Cube设计者注意。

事实表，维度表

1. 这是BI中的概念。各种维度加上都做构成一个事实。比如学生的学号与姓名，加上考试成绩构成一个事实

雪花与星型模型

1. 所谓的雪花模型指一个事实表链接多个维度表，且维度之间存在关系，维度表拥有自己的维度表

2. 所谓的星型模型只一个事实表链接多个维度表，维度表之间没有关系

3. Kylin可以处理星型模型，对雪花模型无能为力（或者需要转换成星型模型）

Cube和Cuboid

1. Cube是一个表中选中参与预计算的所有维度的所有基数的组合总称，而Cuboid是其中的一个组合，所有的Cuboid的总体就是所有的维度的所有基数。

2. 如下面的表，假设我们分析的维度列有两个（也就是该cube中有两个维度列，分别为性别国家），那所有的Cuboid是：【男】，【女】，【中国】，【英国】，【美国】，【男，中国】，【女，中国】，【男，英国】，【女，英国】，【男，美国】，【女，美国】。其中【】就是一个Cuboid，所有的可能的集合就是一个Cube（当然在具体分析中可以对Cuboid进行裁剪，以进行优化）

3. 也就说，Kylin的预计算，就是对度量列的统计，然后group by Cube中的所有Cuboid.

4. 可以想象的，如果维度过多或者维度的基数过高，就会导致Kylin在进行计算时，会将数据膨胀到很大，耗费计算和存储资源。因此如何优化Cube的构建将是优化的突破点

关于表和图的角色分析

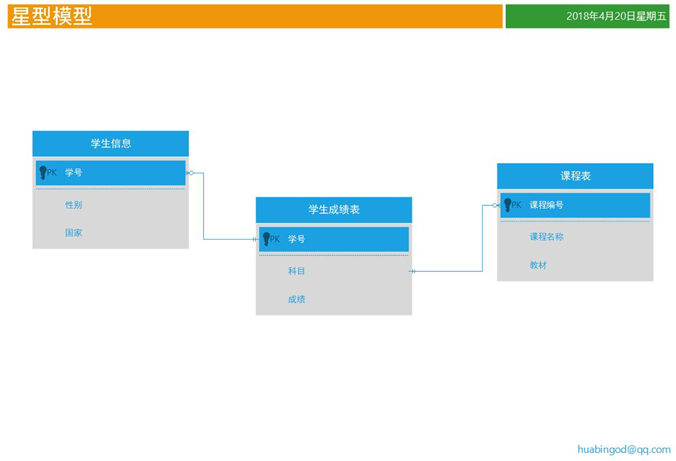
1. 学生信息表和课程表是维度表，学生成绩表是事实表

2. 学生成绩表中的学号和课程编号通常在SQL中被放入group by中，是维度；而成绩经常被sum，avg是度量

3. 如果仅有三张表，那么三张表构成一个星型模型（这里设计的既不符合RDMS的设计要求）；假设在学生信息表的国家并不是国家的名称，而是国家的编码，在另外有一张国家表，专门用来存储国家和国家代码的映射关系。那么学生信息表，学生成绩表，国家表就构成了一个雪花模型。

数据表示例

学生信息表：

学号	性别	国家	姓名
001	男	中国	张三
002	女	英国	李四
003	男	美国	王五

学生成绩表：

学号	课程编号	成绩
001	1	100
001	2	99
002	1	88
002	2	77
003	1	66
004	2	55

课程表

课程编号	课程名称	教材
1	英语	怎么也学不会
2	计算机	从入门到放弃

雪花模型