Docker 核心技术之容器与镜像
Docker容器与镜像的关系

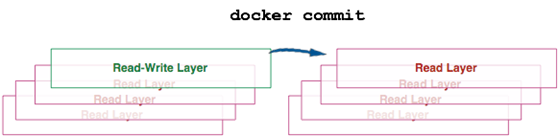
容器提交 – docker commit
docker commit -h
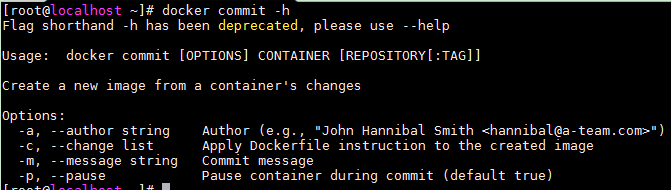
作用:
- 根据容器生成一个新的镜像
命令格式:
- docker commit [OPTIONS] CONTAINER [REPOSITORY[:TAG]]
命令参数(OPTIONS):
- -a, --author string 作者
- -c, --change list 为创建的镜像加入Dockerfile命令
- -m, --message string 提交信息,类似git commit -m
- -p, --pause 提交时暂停容器 (default true)
命令演示 (在d9e 的容器中安装 net-tools 的包)
docker run -dti centos bash docker exec d9e56 yum install -y net-tools docker exec d9e56 ifconfig
把 d9e 的容器重新生成一个新的镜像
docker commit -m 'install net-tools' d9e56 centos-net:v1.0 docker images

查看 镜像 历史记录
docker history centos-net:v1.0

容器导出 – docker export
docker export -h
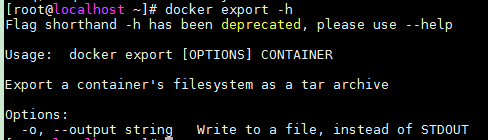
作用:
- 将容器当前的文件系统导出成一个tar文件
命令格式:
- docker export [OPTIONS] CONTAINER
命令参数(OPTIONS):
- -o, --output string 指定写入的文件,默认是STDOUT
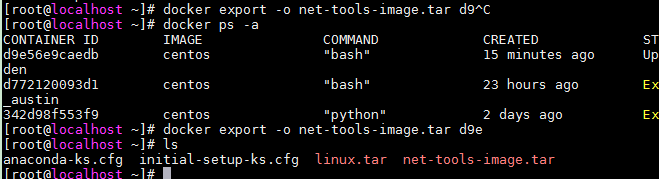
命令演示
docker export -o net-tools-image.tar d9e ls
容器打包的导入 – docker import
docker import -h
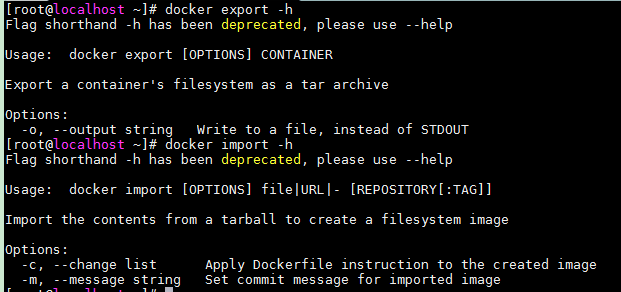
作用:
- 从一个tar文件中导入内容创建一个镜像
命令格式:
- docker import [OPTIONS] file|URL|- [REPOSITORY[:TAG]]
命令参数(OPTIONS):
- -c, --change list 为创建的镜像加入Dockerfile命令
- -m, --message string 导入时,添加提交信息
命令演示
docker import -m '(import) install net-tools' net-tools-image.tar centos2:v1.0

docker history centos2:v1.0

可以看到 import 和 commit 都会生成一个镜像,区别在于import 生成的是一个全新的镜像不保留历史的信息,而 commit 会保留历史的信息,这点可以通过 docker history 去查看
深入理解Docker容器与镜像
镜像的layer
这个可以通过 docker inspect 去查看,每对镜像进行一次修改,都会在Layers 中增加一条记录

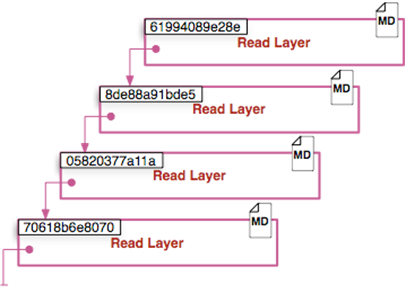
镜像的视角
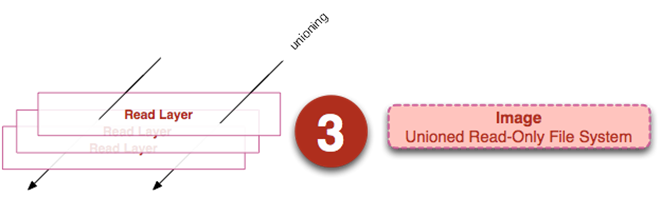
容器的Layer

容器的视角
容器与镜像的底层关系

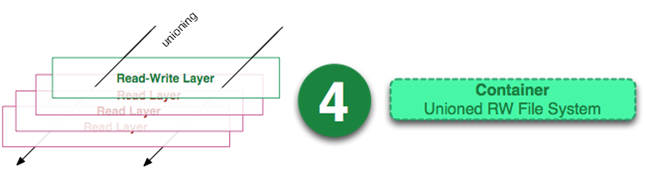
容器的运行
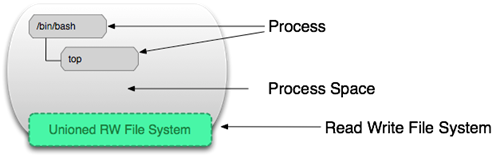
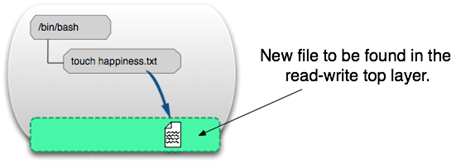
Docker 核心技术之容器与镜像的更多相关文章
- docker 批量删除容器和镜像
docker 批量删除容器和镜像 1,删除单个镜像或者容器 docker rmi 镜像ID/镜像名字:TAG docker rm 容器ID/容器名字 1.停止所有的container,这样才能 ...
- docker入门(二)容器与镜像的理解
10张图带你深入理解Docker容器和镜像 申明:此篇文章是转载的(原文地址http://dockone.io/article/783),今天意外发现已经有人转载了(复制了),希望大家关注原创 原本打 ...
- docker入门(二)容器与镜像的关系
[编者的话]本文用图文并茂的方式介绍了容器.镜像的区别和Docker每个命令后面的技术细节,能够很好的帮助读者深入理解Docker. 这篇文章希望能够帮助读者深入理解Docker的命令,还有容器(co ...
- Docker 核心技术之容器
什么是容器 容器(Container) 容器是一种轻量级.可移植.并将应用程序进行的打包的技术,使应用程序可以在几乎任何地方以相同的方式运行 Docker将镜像文件运行起来后,产生的对象就是容器.容器 ...
- 【docker专栏3】docker基础概念-容器、镜像以及引擎组成部分
一.docker镜像与容器 docker镜像是一个可执行的静态独立软件包,包含打包程序代码和软件运行环境等文件.如:代码.运行时库.环境变量和配置文件等都包含在其中.容器是镜像的运行时状态(镜像中的软 ...
- docker批量删除容器、镜像
1.删除所有容器 docker rm `docker ps -a -q` docker rm $(docker ps -aq) 2.删除所有镜像 docker rmi `docker images - ...
- docker批量删除容器、镜像(转载)
1.删除所有容器 docker rm `docker ps -a -q` 2.删除所有镜像 docker rmi `docker images -q` 3.按条件删除镜像 没有打标签 docker r ...
- Docker 核心技术
docker是什么?为什么会出现? 容器虚拟化技术:轻量级的虚拟机(但不是虚拟机) 开发:提交代码 ——> 运维:部署 在这中间,因为环境和配置,出现问题 ——> 把代码/配置/系统/数据 ...
- docker(一) -- docker安装、容器加速、下载、备份
一.docker的 容器是从镜像中创建出来的虚拟实例 容器用来运行实例,是读写层 镜像用来安装程序,是只读层 1. docker的安装和基本操作 安装命令 yum -y update yum inst ...
随机推荐
- redis使用场景和java测试案例
redis数据结构和使用场景 strings lists sets sort sets hashes strings token session validateCode 分布锁 lists 最近联系 ...
- Jenkins~配合Docker及dotnetCore进行生产和测试环境的灵活部署
回到目录 首先要清楚本文是讲dotnetcore项目在生产和测试环境部署的,这在过去的frameworks项目里,我们可以通过设置web.config的环境变量,然后再发布时指定具体的变量,去实现生产 ...
- springcloud情操陶冶-bootstrapContext(三)
本文则将重点阐述context板块的自动配置类,观察其相关的特性并作相应的总结 自动配置类 直接查看cloudcontext板块下的spring.factories对应的EnableAutoConfi ...
- Spring Cloud Alibaba基础教程:使用Sentinel实现接口限流
最近管点闲事浪费了不少时间,感谢网友libinwalan的留言提醒.及时纠正路线,继续跟大家一起学习Spring Cloud Alibaba. Nacos作为注册中心和配置中心的基础教程,到这里先告一 ...
- JCE安装使用报错
"description":"No key was installed for encryption service","status":& ...
- 【网摘】C#.NET 在 MVC 中动态绑定下拉菜单的方法
1. 已知下拉菜单列表项: 在 Controller 控制器类中输入已下代码 1 public class DemoController : Controller 2 { 3 public ...
- redis的持久化方式RDB和AOF的区别
1.前言 最近在项目中使用到Redis做缓存,方便多个业务进程之间共享数据.由于Redis的数据都存放在内存中,如果没有配置持久化,redis重启后数据就全丢失了,于是需要开启redis的持久化功能, ...
- 学JAVA第十七天,接口与抽象方法
JAVA接口可以让代码更加有合理的规范性,就想一个项目小组,组长要负责把成员的代码整合,但是每个成员写的方式都是按照他们自己的想法来写的, 所以,整合起来就非常麻烦. 但是,如果我们的组长制作了一个接 ...
- 微信小程序 picker 中range-key的坑
<picker class='fr' bindchange="onChangeBuild" range-key="{{'num'}}" value=&qu ...
- 关于HTTPS的简要内容
HTTPS是什么? 超文本传输安全协议(英语:Hypertext Transfer Protocol Secure,缩写:HTTPS,常称为HTTP over TLS,HTTP over SSL或HT ...
