SciTech-Mathematics-Probability+Statistics-PDF:概率密度函数+CDF:累积分布函数-以PoissonDistribution泊松(分类: 条件概率的离散分布)分布为例

原文来自MATLAB R2024A的官方文档：

https://ww2.mathworks.cn/help/stats/poisson-distribution.html

Abbreviations of Statistics:

CDF vs. PDF: What’s the Difference?, BY ZACH BOBBITTPOSTED ON JUNE 13, 2019

• PDF: P.D.F.(Probability Density Function)
• CDF: C.D.F.(Cumulative Distribution Function)

泊松分布 与 二项分布

• 若 \(X ~ B(n,p)\), 当$ n 很大而 p 很小$, \(\lambda = np\)时,
  
  二项分布可用P.D.(Poisson Distribution)近似表示。
• 即\(C_n^k p^k (1-p)^(n-k) = \frac{\lambda ^k}{k!} e^{-\lambda}\)

P.D.(Poisson Distribution, 泊松分布)

• P.D.泊松分布 是一种描述和分析稀有事件的概率分布。样本含量必须很大才能观察到这类事件;

• P.D.泊松分布 实际上是“条件概率离散分布”：以“λ参数的设置(发生)”作为概率的前置条件，
  
  也就是 p.d.f.= f(x|λ)，而且 c.d.f.=F(x|λ) 的原因。

• P.D.泊松分布 更特别的还有它的E(期望)与D(方差)都等于条件概率前置参数λ：
  
  即它的 期望E(x)=λ, 方差D(x)=λ

• P.D.泊松分布 的λ(条件概率前置参数)是 单位测度上的随机事件的平均发生次数,
  
  这里的 “单位测度”可以是单位时间, 单位距离, 单位面积 或 单位体积等；
  
  P.D.泊松分布特别适合于描述单位时间内随机事件发生的次数。

• λ(条件概率前置参数)是泊松分布所依赖的唯一参数,
  
  λ值愈小，分布愈偏倚，随着增大，分布趋于对称。
  
  当 λ=20时, 分布泊松分布接近于正态分布；
  
  当 λ=50时，可以认为泊松分布近似正态分布。
  
  实际工作上，当λ值=20时, 就可以用正态分布来近似地处理泊松分布的问题。

• 已经观测到的场景，包括：

  • 每小时走入商店的人数，
  • 来到某公共汽车站的乘客、
    
    网络上每分钟的丢包数，
    
    盖革计数器每秒咔嗒的次数。
    
    某电话交换台收到的呼叫、

  某放射性物质发射出的粒子、
  
  显微镜下某区域中的白血球等等，
  
  以固定的平均瞬时速率λ（或称密度）随机且独立地出现时，
  
  那么这个事件在单位时间（面积或体积）内出现的次数或个数就近似地服从泊松分布P(λ)。
  
  因此,泊松分布在管理科学、运筹学以及自然科学的某些问题中都占有重要的地位。
  
  （在早期学界认为人类行为是服从泊松分布，2005年在nature上发表的文章揭示了人类行为具有高度非均匀性。）

• 泊松分布广泛应用于：
  
  遗传学的遗传图距计算、
  
  生物物理学的辐射生物学的定量分析、
  
  病毒学中的病毒感染率计算、
  
  分子生物学中一个基因文库所需克隆数的估计、
  
  PCR扩增片段保真率的估算以及酵母单双杂交中转化率的估计等学科领域。

• P.D.由 法国数学家 Siméon-Denis Poisson 在1838年发表.

AI、数据科学和统计(Statistics and Machine Learning Toolbox, MATLAB)

概率分布->离散分布->泊松分布->泊松分布

本页内容

• 概述
• 参数
• PDF概率密度函数
• CDF累积分布函数
• 示例
• 相关分布
• 参考
• 另请参阅
• 相关主题

Main Content

泊松分布

概述

泊松分布是分类为条件概率离散分布的单参数曲线族，

它对随机事件的发生次数进行建模。

此分布适用于涉及计算在给定的时间段、距离、面积等范围内发生随机事件的次数的应用情形。

应用泊松分布的例子，包括每小时走入商店的人数，网络上每分钟的丢包数 以及 盖革计数器每秒咔嗒的次数。

Statistics and Machine Learning Toolbox 提供了几种处理泊松分布的方法。

可通过对样本数据进行概率分布拟合或通过指定参数值来创建概率分布对象 PoissonDistribution。然后使用对象函数来计算分布、生成随机数等。

使用分布拟合器以交互方式处理泊松分布。您可以从该 App 中导出对象并使用对象函数。

将分布特定的函数（poisscdf、poisspdf、poissinv、poisstat、poissfit、poissrnd）与指定的分布参数结合使用。分布特定的函数可以接受多个泊松分布的参数。

将一般分布函数（cdf、icdf、pdf、random）与指定的分布名称 ('Poisson') 和参数结合使用。

参数

PDF概率密度函数

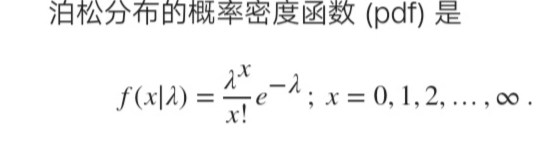
结果是随机事件发生的概率正好是 x。

对于离散分布，pdf 也称为概率质量函数 (pmf)。

有关示例，请参阅计算泊松分布 pdf。

CDF累积分布函数

结果是随机事件发生的概率最多为 x。

有关示例，请参阅计算泊松分布 cdf。

示例

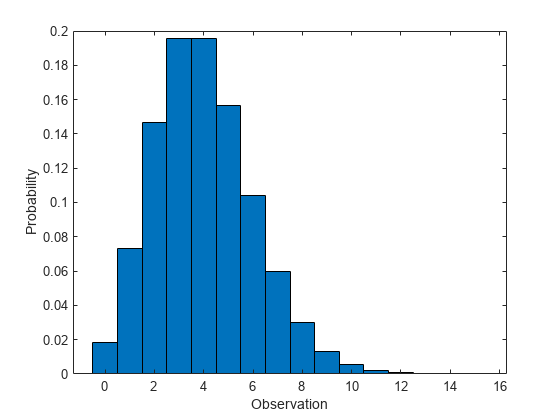
• 计算泊松分布 pdf

  • 计算参数 lambda = 4 的泊松分布的 pdf。
    
    x = 0:15;

y = poisspdf(x,4);



  • 用宽度为 1 的条形绘制 pdf。
    
    figure

bar(x,y,1)

xlabel('Observation')

ylabel('Probability')


    
    

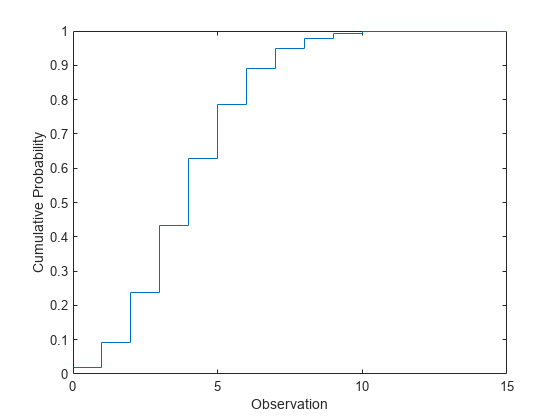
• 计算泊松分布 cdf

  • 计算参数 lambda = 4 的泊松分布的 cdf。
    
    x = 0:15;

y = poisscdf(x,4);



  • 绘制 cdf。
    
    figure

stairs(x,y)

xlabel('Observation')

ylabel('Cumulative Probability')


    
    

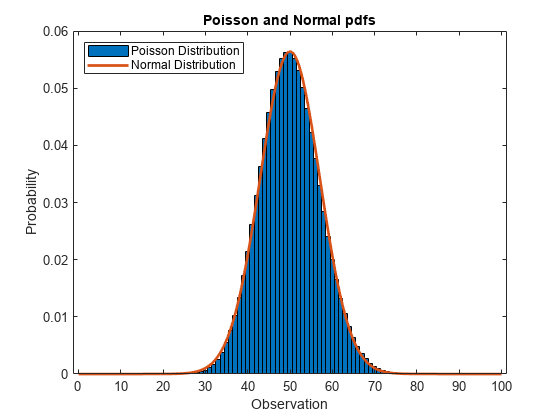
• 比较泊松分布和正态分布的 pdf
  
  当 lambda 较大时，泊松分布可以用均值为 lambda 和方差为 lambda 的正态分布来逼近。

  • 计算参数 lambda = 50 的泊松分布的 pdf。
    
    lambda = 50;

x1 = 0:100;

y1 = poisspdf(x1,lambda);



  • 计算对应正态分布的 pdf。
    
    mu = lambda;

sigma = sqrt(lambda);

x2 = 0:0.1:100;

y2 = normpdf(x2,mu,sigma);



  • 在同一个轴上绘制这些 pdf。
    
    figure

bar(x1,y1,1)

hold on

plot(x2,y2,'LineWidth',2)

xlabel('Observation')

ylabel('Probability')

title('Poisson and Normal pdfs')

legend('Poisson Distribution','Normal Distribution','location','northwest')

hold off


    
    

• 正态分布的 pdf 高度逼近泊松分布的 pdf。

相关分布

• Binomial Distribution - 二项分布是双参数离散分布，它对 N 次独立试验的成功次数进行计数，成功概率为 p。泊松分布是二项分布的极限情况，其中 N 趋向无穷，p 趋向零，而 Np = λ。请参阅Compare Binomial and Poisson Distribution pdfs。

• Exponential Distribution - 指数分布是具有参数 μ（均值）的单参数连续分布。泊松分布对随机事件在给定时间内发生的次数计数进行建模。在这种模型中，事件的时间间隔服从均值为
  
  1
  
  λ
  
  的指数分布。

• 正态分布 - 正态分布是双参数连续分布，具有参数 μ（均值）和 σ（标准差）。当 λ 较大时，泊松分布可以用具有 μ = λ 和 σ2 = λ 的正态分布来逼近。请参阅比较泊松分布和正态分布的 pdf。

参考

[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.

[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8

[3] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.

[4] Loader, Catherine. Fast and Accurate Computation of Binomial Probabilities. July 9, 2000.

另请参阅

PoissonDistribution | poisscdf | poisspdf | poissinv | poisstat | poissfit | poissrnd

相关主题

Working with Probability Distributions

Supported Distributions