字典树Trie详解

哈喽大家好，我是 doooge ，今天给大家带来 Trie 的详解。

\[\Huge \texttt{字典树 Trie 详解}
\]

1.Trie是什么？

Trie 也叫字典树，前缀树，其本质就是一棵字符树。它也是 AC自动机 的一部分。

这是 Trie 的 oiwiki介绍。

Trie 通常用来解决查找一个字符串在某个集合里是否出现过，也可以排序，它的时间复杂度很优秀，\(O(|s|)\) 就可以做到一次查询（\(|s|\) 表示 \(s\) 的长度）。

2.Trie的创建

如果需要在这棵树中查询，就必须要创建这棵树。如果我们要存储 \(ant,bag,bat,cat,car\) 这五个字符串，那么这棵树长这样子：

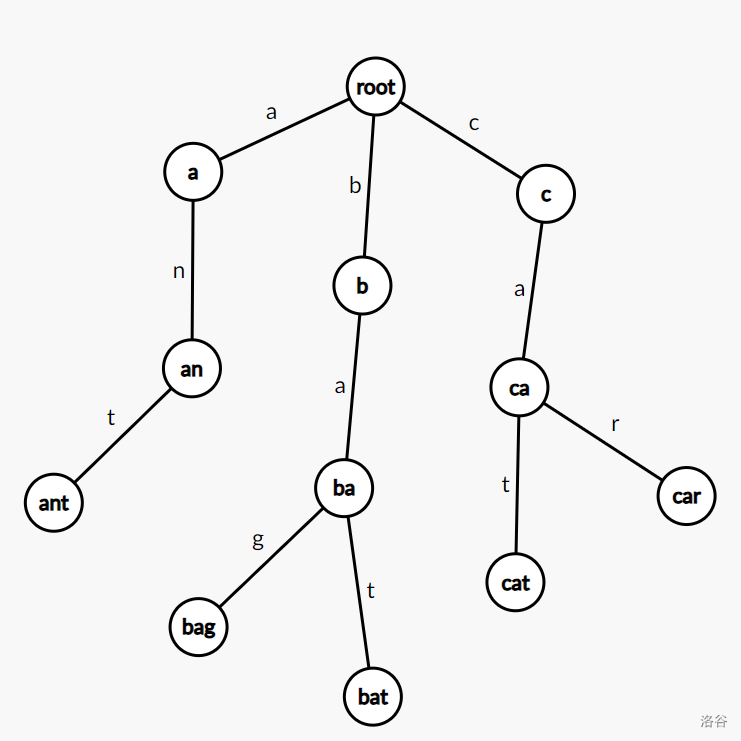
在存储的过程中，我们不必存储每个节点的信息，只要记录它的下一步能到哪里去就行了。在没有字符串存进去的时候，该树只有一个 root 节点。

比如说我们第一个要把 \(bag\) 存进去时，此时这棵树只有一个 root 节点，我们需要建立一条边 \(b\)，将 \(b\) 节点存进去。之后我们需要建立一条边 \(a\)，将 \(ba\) 节点存进去，以此类推，直到存到 \(bag\) 节点为止。

再比如说，我们第一个要把 \(bat\) 存进去时，此时这棵树已经有了 \(b,ba\) 节点，我们不需要建立一条新边，只要往下搜即可。到了 \(ba\) 节点，因为没有 \(bat\) 节点，所以得建立一条边 \(t\)，把 \(bat\) 节点存上去。

当然，当一些题目需要询问存进去了哪些串时，需要加一个标记或者计数数组（这取决于该题是否要给它们计数），当存完了时打上标记即可。

这样，一棵 Trie 树就建好了，建树的时间复杂度为：

\[O(\sum_{i=1}^{n} |s_i|)
\]

3.Trie的查询

Trie的查询很好懂。

比如说刚才图片中的树，我们要查询 \(cat\) 是否在树中出现，就只要变搜边看即可。我们得从 root 节点搜起，用 \(pos\) 变量记录搜到哪了，\(pos\) 初始为 \(0\)，也就是 root 节点的编号。

可以发现，root 节点有一条边连着 \(c\) 节点，因为 \(cat\) 的第 \(1\) 项为 \(c\)，那么就将 \(pos\) 设为 \(c\) 节点的编号，继续搜下去。\(c\) 节点有一条边连着 \(a\) 节点，因为 \(cat\) 的第 \(2\) 项为 \(a\)，那么就将 \(pos\) 设为 \(a\) 节点的编号，继续搜下去。

以此类推，直到我们搜完 \(cat\) 这个字符串。可以发现，该字符串确实存在，我们就搜完了。

再比如我们要搜索 \(can\) 这个字符串，跟 \(cat\) 差不多，但当我们搜索到 \(ca\) 这个节点时，因为这个节点并没有 \(t\) 这条边，所以搜不到，返回 \(-1\)。当发现搜不到时，返回 -1。

搜 \(n\) 次树的复杂度为：

\[O(\sum_{i=1}^{n} |s_i|)
\]

是不是发现建树和搜树差不多？于是就有了一些边建边搜的题。

4.Trie的代码实现

相信你如果读懂了 Trie 建树搜树的过程，一定能自己手打了把。当然不会的也没关系，看这里：

建树：

void build(string s){
	int pos=0,len=s.size();
	for(int i=0;i<len;i++){
		if(!nxt[pos][s[i]-'a']){
			nxt[pos][s[i]-'a']=++cnt;
		}
		pos=nxt[pos][s[i]-'a'];
	}
	f[pos]=true;
}

搜树：

int find(string s){
	int pos=0,len=s.size();
	for(int i=0;i<len;i++){
		if(!nxt[pos][s[i]-'a'])return -1;
		pos=nxt[pos][s[i]-'a'];
	}
	if(!f[pos])return -1;
	return 1;
}

5.Trie的例题

例题1：于是他错误的点名开始了

题目大意：给你 \(n\) 个字符串组成的一个集合，\(m\) 次询问，每次询问给出一个字符串，问你该串是否在集合里出现过，若没出现过，输出 WRONG。如果之前询问点过名，输出 REPEAT。否则输出 OK。

虽然这题用 map 也可以 AC，但是这也是一道非常适合 Trie 的板子题。

思路：我们维护一个前缀树，再用一个标记数来统计是否出现过就可以了。

代码：

#include<bits/stdc++.h>
#define code return
#define by 0
#define doooge ;
using namespace std;
int nxt[500010][30],cnt;
bool f[500010],f2[500010];//判断是否出现过
void build(string s){
	int pos=0,len=s.size();
	for(int i=0;i<len;i++){
		if(!nxt[pos][s[i]-'a']){
			nxt[pos][s[i]-'a']=++cnt;
		}
		pos=nxt[pos][s[i]-'a'];
	}
	f[pos]=true;
}
int find(string s){
	int pos=0,len=s.size();
	for(int i=0;i<len;i++){
		if(!nxt[pos][s[i]-'a'])return -1;
		pos=nxt[pos][s[i]-'a'];
	}
	if(!f[pos])return -1;
	if(f2[pos])return 0;
	f2[pos]=true;
	return 1;
}
int main(){
	int n,m;
	cin>>n;
	for(int i=1;i<=n;i++){
		string s;
		cin>>s;
		build(s);
	}
	cin>>m;
	while(m--){
		string s;
		cin>>s;
		int res=find(s);
		if(res==-1)cout<<"WRONG\n";
		else if(res==0)cout<<"REPEAT\n";
		else cout<<"OK\n";
	}
	code by doooge
}

例题2：【模板】字典树

思路：这题与我们将的 Trie 有所不同的是他需要计数有多少个子串，这时我们就可以用一个计数数组来代替标记数组就可以了。注意判断大小写。

注意初始化别用 memset，特别慢。

代码：

#include<bits/stdc++.h>
#define code return
#define by 0
#define doooge ;
using namespace std;
int nxt[3000010][70],cnt;
int sum[3000010];
int get(char c){
	if(c>='0'&&c<='9')return 52+c-'0';
	return (c<'a'?26+c-'A':c-'a');
}
void build(string s){
	int pos=0,len=s.size();
	for(int i=0;i<len;i++){
		if(!nxt[pos][get(s[i])]){
			nxt[pos][get(s[i])]=++cnt;
		}
		pos=nxt[pos][get(s[i])];
		sum[pos]++;
	}
}
int find(string s){
	int pos=0,len=s.size();
	for(int i=0;i<len;i++){
		if(!nxt[pos][get(s[i])])return 0;
		pos=nxt[pos][get(s[i])];
	}
	return sum[pos];
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--){
		for(int i=0;i<=cnt;i++){
			for(int j=0;j<=66;j++)nxt[i][j]=0;
		}
		for(int i=1;i<=cnt;i++)sum[i]=0;
		cnt=0;
		int n,m;
		cin>>n>>m;
		for(int i=1;i<=n;i++){
			string s;
			cin>>s;
			build(s);
		}
		while(m--){
			string s;
			cin>>s;
			cout<<find(s)<<'\n';
		}
	}
	code by doooge
}

6.作业

作业T1：

阅读理解，难度：\(2■■□□□\)，虽然 map 也可以做，但是这题也算一道 Trie 板子题。

作业T2：

前缀统计，难度：\(3■■■□□\)，跟例题2的思想差不多。

作业T3：

会议座位，难度：\(5■■■■■\)，需要求逆序对。

7.闲话

下一篇文章将讲 Trie的变种：01-Trie和Trie的合并，还有可持久化Trie，期待一下！

蒟蒻不才，膜拜大佬。如果文章错了字或代码，请在评论区@我。