2025杭电多校第一场 树上lcm、子序列、传送门个人题解

传送门

dijkstra

题目

思路

这题很明显是一个最短路问题，但是其中的限制条件比较特殊，每个边都有自己的颜色，在更新当前节点的时候需要考虑上一个节点的信息。

我们开的结构体\(edge\)存边时要记录其颜色\(c\)；

给每个节点都开一个\(set\)用于储存到达这个节点路径最短的边都有哪些颜色；

开数组\(vis[N]\)用于跑dijkstra，\(dp[N]\)记录最短路

struct edge {
    vector<pair<ll, ll>>e;//c,next
}a[N];

set<int>last[N];
int vis[N], dp[N];

设当前节点为\(u\)，需要更新的节点为\(next\)，\(u \xrightarrow{id}next\)所连的边的颜色为\(id\)

• 若\(last[next].count(id)\)，由于dijkstra只会让\(next\)入队一次，说明\(next\)在之前被更新为最短路的时候已经算上了变换颜色的额外路径，当前的\(id\)在计算路径的时候就不需要加上路径了
• 若\(!\,last[next].count(id)\)，说明\(next\)更新的最短路中不包含颜色\(id\)，此时计算路径的时候就需要加上变换颜色的额外开销了

代码实现

#include<iostream>
#include<vector>
#include<cstdio>
#include<set>
#include<queue>
#include<algorithm>
#include<cmath>
using namespace std;
#define ll long long
#define rep(i,a,b) for(ll i=(a);i<=(b);i++)
#define per(i,a,b) for(ll i=(a);i>=(b);i--)
#define see(stl) for(auto &ele:stl)cout<<ele<<"\n"; cout<<'\n';
#define endl '\n';

const ll inf = 1e9;
const int N = 2e5 + 5;

struct edge {
    vector<pair<ll, ll>>e;//c,next
}a[N];

set<int>last[N];
int vis[N], dp[N];

void dj(int s) {
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>dq;
    dp[s] = 0;
    dq.push({ 0,s });
    while (!dq.empty()) {
        int u = dq.top().second;
        dq.pop();
        if (vis[u])continue;
        vis[u] = 1;
        for (auto& son : a[u].e) {
            int id = son.first, next = son.second;
            if (last[next].count(id)) {
                if (dp[next] == dp[u]) {
                    if (!vis[next])dq.push({ dp[next],next });
                }
                else if (dp[next] > dp[u]) {
                    dp[next] = dp[u];
                    last[next].clear();
                    last[next].insert(id);
                    if (!vis[next])dq.push({ dp[next],next });
                }
            }
            else {
                if (dp[next] == dp[u] + 1) {
                    last[next].insert(id);
                    if (!vis[next])dq.push({ dp[next],next });
                }
                else if (dp[next] > dp[u] + 1) {
                    dp[next] = dp[u] + 1;
                    last[next].clear();
                    last[next].insert(id);
                    if (!vis[next])dq.push({ dp[next],next });
                }
            }
        }
    }
}

void eachT() {
    int n, m; cin >> n >> m;
    rep(i, 1, n)dp[i] = inf, vis[i] = 0, last[i].clear(), a[i].e.clear();
    rep(i, 1, m) {
        int u, v, c; cin >> u >> v >> c;
        a[u].e.push_back({ c,v });
        a[v].e.push_back({ c,u });
    }
    dj(1);
    cout << dp[n] << '\n';
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)eachT();
    return 0;
}

---

子序列

贪心

题目

思路

来自小组成员phaethon90

本题的关键在于“排列”二字，由此可以知道\(1\sim n\)均出现且只出现一次。

若给定子序列的两个端点\([l,r]\)，中间则最多有\(min\{ a[l],a[r] \}-1\)个数满足条件，此时只要知道有多少个小于\(min\{ a[l],a[r] \}\)的数不在\([l,r]\)中国，利用差值即可\(O(1)\)算出最大长度

用双指针\(l,r\)数组的两端遍历：

由于长度上限与\(min\{ a[l],a[r] \}\)有关，因此每次都移动所指的值较小的那个指针，直到遇到比原端点更大的值（小值对答案的更新没有贡献）

注意到此时区间外的点的值均小于现在两个指针所指的值，于是可以\(O(1)\)算出子序列的最大长度并更新答案

最后需要注意一下特判\(n==1\)的情形

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i++)
#define per(i, a, b) for(ll i = (a); i >= (b); i--)
//#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
#define double long double

const int N=2e6+5;
int a[N];
void solve() {
	int n;cin>>n;
	rep(i,1,n)cin>>a[i];
	if(n==1){cout<<1<<'\n';return;}
	int cnt=-1,l=1,r=n,ans=0;
	while(l<r){
		ans=max(ans,min(a[l],a[r])-(++cnt)+1);
		if(a[l]<a[r])l++;
		else r--;
	}
	cout<<ans<<'\n';
}
int main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	int t = 1;
	cin >> t;
	while (t--) solve();
	return 0;
}

---

树上LCM

树上dp dp 子集合dp

思路

fishergo大佬在赛时用莫比乌斯反演过了本题，但本蒟蒻到现在还没学明白

由\(lcm\)的性质，我们很容易推出结论：

• 设节点\(u\)的值为\(a[u]\)，若\(lcm(a[u],x)>x\)，则点\(u\)必定不能再路径中
• 所有能够到达的点的值必定是\(x\)的因数

将\(x\)质因数分解为\(q_{1}^{p_{1}}q_{2}^{p_{2}}\dots q_{k}^{p_{k}}\)，由于\(x\leq 1e7\)，则\(k\leq 7\)

此时所有合法的点的值\(a[u]\)都可以表示为\(q_{1}^{u_{1}}q_{2}^{u_{2}}\dots q_{k}^{u_{k}}\)，只有在\(u_{i}==p_{i}\)的时候，\(u\)才算作对\(lcm\)贡献了因数\(q_{i}^{p_{i}}\)（如\(x=2^3·3^2\)，\(a[u]=2^3\)时对\(lcm\)的\(2^3\)因数有贡献，\(a[v]=2^2·3\)时对\(lcm\)没有任何贡献）

由于每个质因数的幂次这个整体\(q_{i}^{p_{i}}\)要么有贡献要么没有贡献，因此可以对\(q_{1}^{p_{1}}q_{2}^{p_{2}}\dots q_{k}^{p_{k}}\)状态压缩为位数为\(k\)的二进制数，\(1\)代表有这个因数整体，\(0\)代表没有（如\(x=2^3·3^2·5^4\)，\(a[u]=2^3·5^4\)压缩后为\(101(2)\) ）

因此我们将所有的\(a[u]\)状态压缩，合法的就将压缩后的十进制数存为\(state\)，不合法的存为\(-1\)

接下来进行树上dp：

状态含义：

\(f[u][state]\)表示以节点\(u\)为根的子树中，以\(u\)为端点的路径的\(lcm\)状态压缩后为\(state\)的路径数

\(dp_{u}[state]\)表示当前状态下，\(u\)已经处理完的子树中，以\(u\)为端点的路径的\(lcm\)状态压缩后为\(state\)的超集的路径数

超集：若\(i|j=i\)，则称\(j\)为\(i\)的子集，\(i\)为\(j\)的超集

状态转移：

预处理超集和：

\[\begin{align}
&if(\ !(j>>1\&1)\ ) : \\ \\
&dp_{u}[j]+=dp_{u}[\ j\wedge(1< < i)\ ]
\end{align}
\]

树上dp：

\[\begin{align}
&newstate=i\ |\ a[u].state \\ \\
&ans+=dp_{u}[\ newstate\wedge one\ ]\times f[son][i]\\ \\
&f[u][x]+=f[son][i]
\end{align}
\]

其中\(one\)代表二进制表示为全1的数

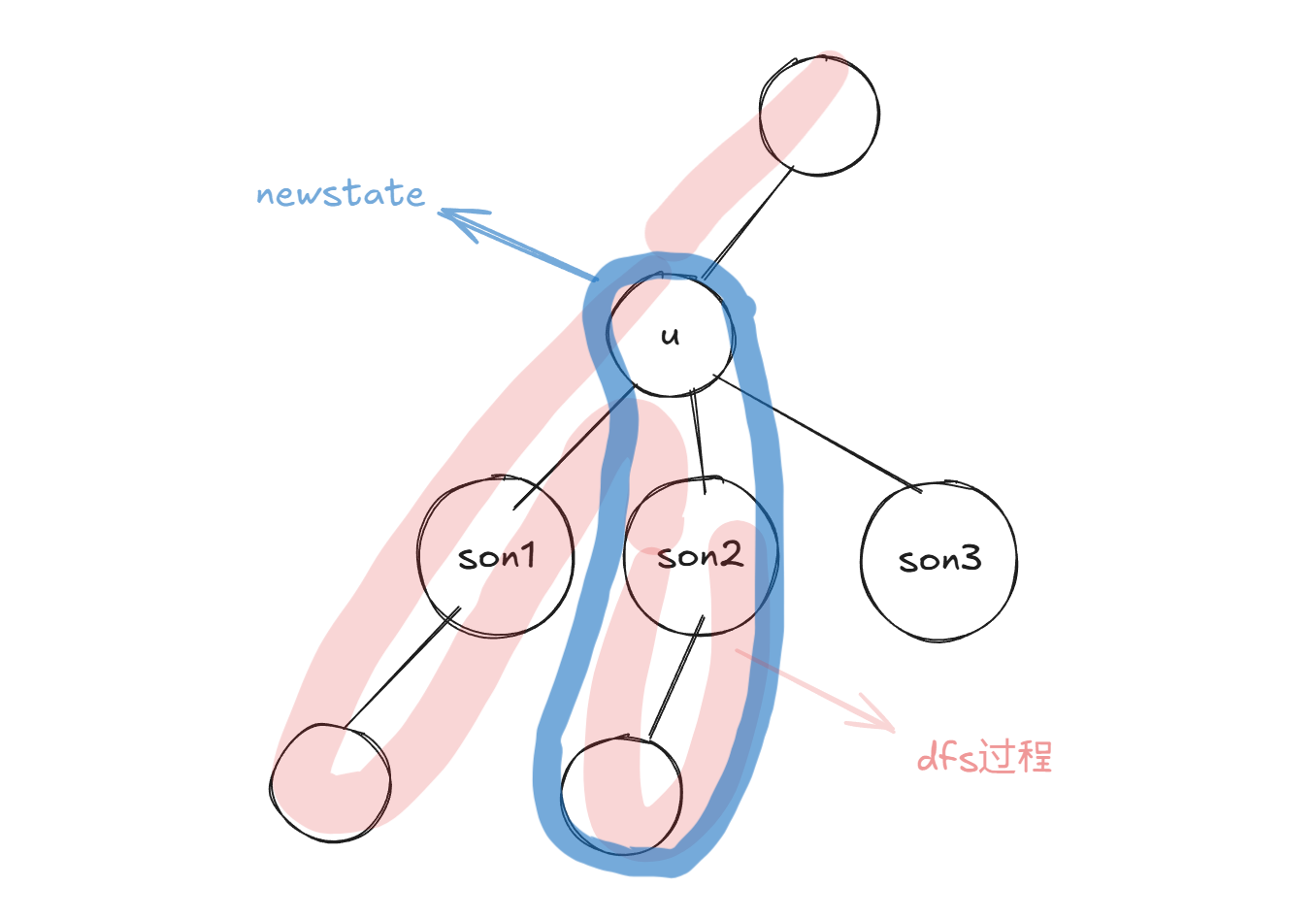
预处理超集和的过程可以参考文章：高维前缀和

在dfs回溯的过程进行树上dp

遍历从\(son\)中传回来的所有状态压缩的数\(i\)，与当前点\(u\)的状态压缩数\(a[i].state\)作或运算，可得\(son\)所在子树中某条状态为\(i\)的路径多加上\(u\)点后的新状态\(newstate=i\ |\ a[u].state\)

现在的目标便是在已处理的子树（图中红色部分）中找到一些包含节点\(u\)的路径，使得这些路径和蓝色路径拼接起来后的\(lcm\)为\(x\)，即这两部分的状态在或运算后为\(one\)

因此找出\(newstate\)的补集\(newstate \wedge one\)，其超集与\(state\)或运算后必然是\(one\)

蓝色部分的路径个数为\(f[son][i]\)，红色部分的路径个数为\(dp[\ state \wedge one\ ]\)，二者相乘即可算出对答案的贡献

最后，\(a[u].state\)本身就是\(one\)的情况需要特判

代码实现

#include<iostream>
#include<vector>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(ll i = (a); i <= (b); i++)
#define per(i, a, b) for(ll i = (a); i >= (b); i--)
#define mid ((l+r)>>1)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';

vector<ll>prime, vis;
void sieve(ll len) {
    vis.assign(len + 1, 0);
    prime.push_back(0);
    rep(i, 2, len) {
        if (!vis[i])prime.push_back(i);
        for (ll j = 1; i * prime[j] <= len && j < prime.size(); j++) {
            vis[prime[j] * i] = 1;
            if (i % prime[j] == 0)break;
        }
    }
}
vector<int>cnt, fac;
int len,one;
ll gcd(ll a, ll b) {
    if (b == 0)return a;
    return gcd(b, a % b);
}
ll lcm(ll a, ll b) {
    return a * b / gcd(a, b);
}

const int N = 1e5 + 5;
int n, x;
struct node {
    vector<int>e;
    int val, state;
}a[N];

vector<ll>f[N];
ll ans;

int get(int y) {
    if (lcm(x, y) != x)return -1;
    int val = 0, j = 0;
    rep(i, 0, len - 1) {
        int cur = 0;
        while (y % fac[i] == 0) {
            y /= fac[i];
            cur++;
        }
        if (cur == cnt[i])val |= (1 << j);
        j++;
    }
    return val;
}

void dfs(int u, int fa) {
    int val = a[u].val;
    a[u].state = get(val);
    f[u].resize(one+1,0);
    for (auto& son : a[u].e) {
        if (son == fa)continue;
        dfs(son, u);
    }
    if (a[u].state == -1)return;
    f[u][a[u].state] = 1;
    for (auto& son : a[u].e) {
        if (son == fa)continue;
        vector<ll>dp = f[u];
        rep(j, 0, len - 1) {
            rep(i, 0, one) {
                if (!(i >>j & 1))dp[i] += dp[i ^ (1 << j)];
            }
        }
        rep(i, 0, one) {//f[son][i]
            int state = i | a[u].state;
            ans += dp[state ^ one] * f[son][i];
            f[u][state] += f[son][i];
        }
    }
    if (a[u].state == one)ans++;
}

void init() {
    ans = 0;
    rep(i, 1, n)a[i].e.clear(), a[i].state = 0,f[i].clear();
    cnt.assign(10, 0), fac.assign(10, 0);
}

void solve() {
    cin >> n >> x;
    init();
    int pos = 0, tmp = x;
    rep(i, 1, prime.size() - 1) {
        if (prime[i] > x)break;
        if (tmp % prime[i] == 0) {
            fac[pos] = prime[i];
            while (tmp % prime[i] == 0) {
                tmp /= prime[i];
                cnt[pos]++;
            }
            pos++;
        }
    }
    len = pos; one = ((1 << (len)) - 1);
    rep(i, 1, n - 1) {
        int u, v; cin >> u >> v;
        a[u].e.push_back(v);
        a[v].e.push_back(u);
    }
    rep(i, 1, n)cin >> a[i].val;
    dfs(1, 0);
    cout << ans;
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    sieve(1e7);
    int t = 1;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}