codeup之分数序列求和

Description

有如下分数序列

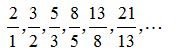
求出次数列的前20项之和。

请将结果的数据类型定义为double类型。

Input

无

Output

小数点后保留6位小数，末尾输出换行。

Sample Input Copy

无

Sample Output Copy

32.660261

idea

数列的规律：
分子为前一项分子分母的和
分母为前一项的分子

solution

#include <stdio.h>
int main(){
	double f1 = 1.0, f2 = 2.0, sum = 0, temp, t;
	for(int i = 0; i < 20; i++){
		temp = f2 / f1;
		t = f2;
		f2 = f1 + f2;
		f1 = t;
		sum += temp;
	}
	printf("%.6f", sum);
	return 0;
}