HDU 4579 Random Walk （解方程组）

Random Walk

Time Limit: 5000/2000 MS (Java/Others)    Memory Limit: 65535/65536 K (Java/Others)
Total Submission(s): 81    Accepted Submission(s): 35

Problem Description

Yuanfang is walking on a chain. The chain has n nodes numbered from 1 to n. Every second, he can move from node i to node j with probability:

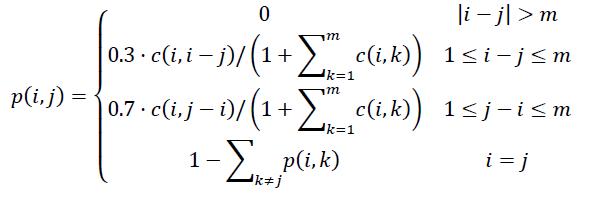
c(i,j) is an element in a given parameter matrix which is n×m. (1 <= c(i, j) <= 9)
Yuanfang wants to know the expectation time for him to walk from node 1 to node n.

 

Input

There are no more than 10 test cases.
In each case, there are two integers n (2 <= n <= 50000), m (1 <= m <= 5), in the first line, meaning that there are n nodes and the parameter matrix is n×m . There are m integers in each of the next n lines which describe the parameter matrix .
The input ends with 0 0.

 

Output

For each case, output the expectation time for Yuanfang to walk from node 1 to node n in one line. The answer should be rounded to 2 digits after decimal point.

 

Sample Input

3 1
1
1
1
5 2
1 2
2 1
3 2
2 3
1 3
0 0

 

Sample Output

6.94
8.75

 

Source

2013ACM-ICPC杭州赛区全国邀请赛

 

 

 

 

 

这题就是列出方程。

 

然后高斯消元解方程。

 

如果是一般的方程，高斯消元需要O(n*n)

 

但是这题的矩阵很特别

 

 

很快就可以消掉了。

用dp[i]表示i到n的期望。

dp[n]=0;

 

 

对于第i个方程，最多只有2*m+1个系数是不为0的。

 

 

 

 

 

 /* **********************************************
 Author      : kuangbin
 Created Time: 2013/8/12 20:28:58
 File Name   : F:\2013ACM练习\比赛练习\2013杭州邀请赛重现\1004.cpp
 *********************************************** */

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <string>
 #include <math.h>
 #include <stdlib.h>
 using namespace std;
 const int MAXN = ;
 double c[MAXN][];
 double p[MAXN][];
 double a[MAXN][];
 double b[MAXN];
 double dp[MAXN];

 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
     int n,m;
     while( scanf("%d%d",&n,&m) ==  )
     {
         if(n ==  && m == )break;
         for(int i = ;i <= n;i++)
             for(int j = ;j <= m;j++)
                 scanf("%lf",&c[i][j]);
         for(int i = ;i < n;i++)
         {
             double sum = ;
             for(int j = ;j <= m;j++)
                 sum += c[i][j];
             double s = ;
             for(int j = ;j <= m && i-j >= ;j++)
             {
                 p[i][m-j] = 0.3*c[i][j]/(+sum);
                 s += p[i][m-j];
             }
             for(int j = ;j <= m && i+j <= n;j++)
             {
                 p[i][m+j] = 0.7*c[i][j]/(+sum);
                 s += p[i][m+j];
             }
             p[i][m] = -s;
             b[i] = -;
         }
         for(int i = ;i <= m+ && i <= n;i++)
             a[][i] = p[][m+i-];
         for(int i = ;i < n;i++)
         {
             int end = min(i+m,n);
             int start = max(,i-m);

             for(int j = start;j < i;j++)
                 if(fabs(p[i][m+j-i]) > 1e-)
                 {
                     double t = p[i][m+j-i]/a[j][];
                     for(int k = ; k <= m+ && j+k- <= n ;k++)
                     {
                         p[i][m+j-i+k-] -= t*a[j][k];
                     }
                     b[i] -= t*b[j];
                 }
             for(int j = ;j <= end-i+;j++)
                 a[i][j] = p[i][m+j-];

         }
         dp[n] = ;
         for(int i = n-;i >= ;i--)
         {
             for(int j = ;j <= m+ && i+j- <= n;j++)
                 b[i] -= dp[i+j-] * a[i][j];
             dp[i] = b[i]/a[i][];
         }
         printf("%.2f\n",dp[]);
     }
     return ;
 }