[数学趣味001]RSA算法原理及示例

可以先看看这个视频： RSA_Encryption_Algorithm

公开密钥

Perwork:
私钥：Sender和Receiver预先约定加密和解密方案，向其他人保密。

这个实现比较难：向其他人保密。假如你是个商家，很多人要和你联络，发送者可能和你一点关系也没有，怎么保密。

需求：Sender素不相识，发送消息需求保密，加密方案必须公开。【就和信箱一样，所有人都可以向你公开的的信箱里投信件，但是只有你才有钥匙(私有的)取信件】

公钥：加密方案向所有人公开，解密方案只有Receiver知道，对其他所有人(包括Sender),Sender和除Receiver外所有人都是平等的，【Sender把信件放入Receive信箱了，Sender就不能再看到信件内容啦】

这就要求加密很容易，但是解密很难的算法！从跳板里跳入水里容易，想跳回去就不是那么容易啦。

先用一下示例讲下流程：

---

1. 定义一个信息集合

Zset={0,1,2,3,...90}.

这个就是相当于26个英文字母，只要知道这26个字母，你就可以拼出任何想要的信息，只是我们把26个扩展为了91个。

2. Sender 要发送的信息为

%%现实生活中：
Msg = ”晚上一起吃饭”;
%%等价为信息集合里是：只要Reciver得到的内容最终为{1,2,3,4,5,6}就可以知道是现实的“晚上一起吃饭”
Msg ={1,2,3,4,5,6};

这里的Msg就是一个明文。

3. Sender 把信息编码为明文后，还要进行加密！

把明文的每一个元素都映射为另一个唯一的值(密文：可以公开的值)

%%明文
Msg = {1,2,3,4,5,6};
%%使用加密：C = A^5(mod 91)
%%A^5 -->
NewMsg = {1,32,243,1024,3125,7776}
%%mod 91  对91取余得到密文
NewMsg = {1,32,61,23,32,41};

简单来说：加密过程为：

%%  明文             公式:5次方后对91取余         密文
     A -------------> A

⁵

 mod 91 -------------->C

最后的保证：A和C绝对是一对一映射关系。

Question1: 那么这个密文怎么保证不被破解呢？

我们试下从这公开的加密公式和密文反推之

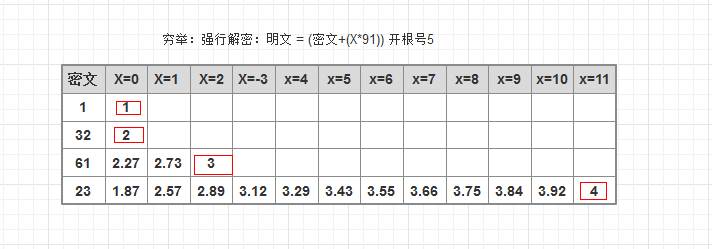
可以看出，通过穷举，我们还是可以得到结果的，但这个计算次数也是指数增长的，且计算开根号得整数操作很要耗时，

一个算法最后逼得人只能用穷举来解密，那么就是成功啦，

思考：如果公式里面不是5次方，而是三位数，四位数的次方，那计算量就更大。

3 . sender把这密文发给Receiver 加密工作完成

4. 解密：Receive知道信息比Sender多的就是这个91是怎么来的，这个是关键。

4.1 91 = 7*13 (实现应用中，会设定为2个非常大的素数相乘，让Sender看不出是哪2个素数来，我们为了演示简单，假定Sender不会得到91=7*13这个结果，只有Receiver知道)

这个算法就是利用了这一点：2个素数乘积的结果很容易，但是想反过来把结果反推为哪2个素数相乘很难。所有公开密钥都是正着做容易，反过来就是很难

4.2 根据费马小定理：和辗转相除法可以得到：

5d = 1+(13-1)*(7-1)*k

从以上可以“容易穷举出一个”k=2时 ：5*29 = 1+（13-1）*（7-1）*2

4.3 接着我们对密文C再乘29次方后对91取余就可以直接得到明文啦

你只要知道那个29，就可以得到破解啦！！！！！

是不是很神奇！！！！！！当然我们还是有很多迷惑的，比如：

为什么选5，91，这些数字有什么要求？接下来，我们先理一下上面的步骤:

步骤	示例
取2个大质数：p,q	p=7,q=13
密钥:n=p*q,h 是一个与(p-1)(q-1)互质的数, 公开n 和 h ,p,q不公开	n =91，h = 5（与72互质）
加密（公开）C = Ah (mod n)	A = 明文,h=5,n=91,C= 密文
解密（保密）hd = 1+(p-1)(q-1)k---->A = C d mod 91	5d = 1+72*k, 当k=2时，d=29成立
解密完成	密文乘方29 再对91取模 得到明文

原理证明 ：

1. 取2个很大的不相等的质数p,q ;

2. m = p*q

3. 根据欧拉函数：比m小的质数个数r = φ(N) = φ(p)*φ(q) = (p-1)*(q-1)

4. 选取一个与R互质的数e

5. 根据欧几里德(辗转相除)定理：2个互质的数一定满足：e*x – r*y =1;

6. 上式等价为： e*d – r*k = 1;

7.密文c ,明文a , 加密 a ^e = c (mod m);

8. 解密： c ^d = a (mod m),这个结论是 我们要证明的，

9. c^d = a^e*d = a ^1+r*k =a*a ^r*k

所以只要证明： a*a ^r*k = a(mod m) ---->a ^r*k = 1 (mod m)

10 .根据费马小定理:

:

a ^r*k = (a ^k)^r = 1 （mod m).

---

数学真有意思…….