cogs——2478. [HZOI 2016]简单的最近公共祖先

2478. [HZOI 2016]简单的最近公共祖先

★☆   输入文件：easy_LCA.in   输出文件：easy_LCA.out   简单对比
时间限制：2 s   内存限制：128 MB

【题目描述】

给定一棵有n个节点的有根树，根节点为1，每个节点有一个权值wi，求

即求所有无序节点对的LCA的权值之和。

树的节点编号为1~n，LCA表示两节点的最近公共祖先，即在它们的所有公共祖先中离根节点最远的节点。

【输入格式】

第一行一个整数n，表示节点数。

第二行n个正整数，表示每个点的权值。

以下n-1行每行两个整数x,y，表示树上有一条边连接节点x和节点y。

【输出格式】

一个整数，表示答案。

【样例输入】

3
1 2 3
1 2
1 3

【样例输出】

9

【数据范围与约定】

对于30%的数据，n<=1000。

对于60%的数据，n<=100000。

对于100%的数据，1<=n<=1000000，0<wi<=1000000。

【来源】

HZOI 2016

思路：

看到这个题我上来就写lca然后·成功的T成了狗、、、、

呜呜呜~~~~(>_<)~~~~

某位大佬说这个题要用dfs+乱搞，然后就可以A掉、、、

至于怎么来做，我们看下面的分析

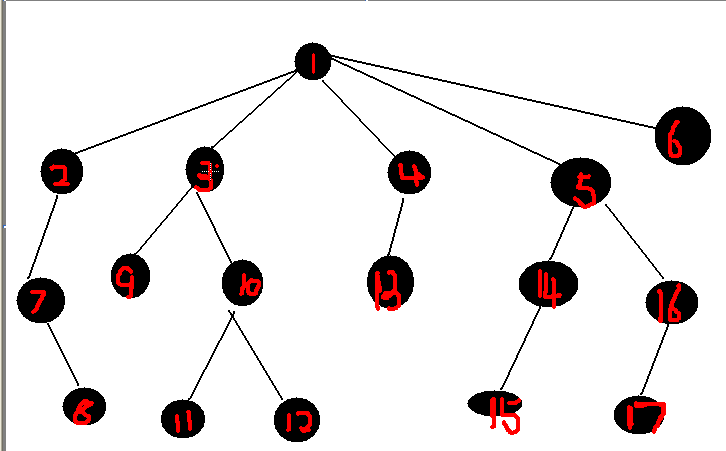我们来看一下左图。

首先，我们枚举每一个lca，然后判断他里面有几个节点（某大佬：其实不用枚举的，我们直接dfs就好了，这样什么都出来了、、、）

好，我们按照这位大佬的思路来、、、

我们先从1号节点来枚举，看下图

在这里我们先从一号节点开始，找与他相连的子树，在这里为了方便，我们先给它标上号，一号节点一共有5颗子树，首先，我们知道，1号节点与1号子树内的所有节点的最近公共祖先是1号节点本身对吧？！既然这样，我们可以组出来1*3个组合对吧？！也就是说现在我们一共有1*3个节点以1号节点为lca

然后我们再看下图。

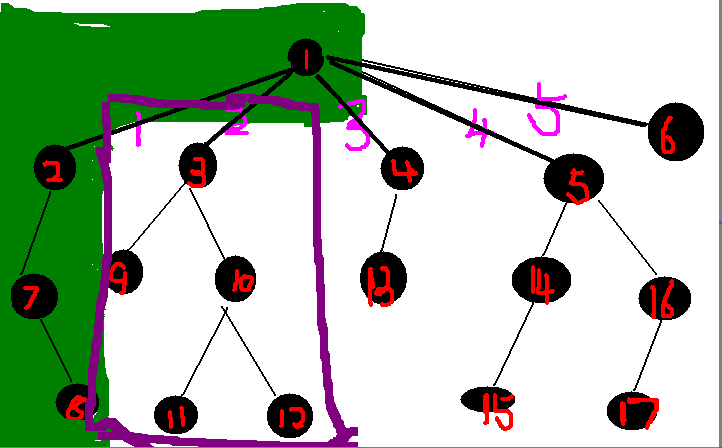然后我们知道1号节点和1号子树内的点跟2号子树内的点的lca一定是1号节点对吧，既然如此我们就把1号节点与1号子树内的节点个数合并起来，也就是4，这4个节点与2号节点内的4个点的lca仍为1

以此类推，我们把合并起来的1号子树在与2号子树合并，然后他们与3号子树的lca仍然是1号节点、、、、、

这样，我们就可以得到所有的lca权值之和。

但是我们发现，我们这个题里有lca（i，i）这样的点对吧，我们肯定知道这样的点的lca就是他本身，然后我们最后求解出ans后枚举每一个点再将他们的权值加上就好了！

代码：

#include<cstdio>
#include<vector>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 1000010
using namespace std;
vector<int>vec[N];
int n,x,y;
];
int read()
{
    ,f=; char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
int dfs(int x)
{
    deep[x]=deep[fa[x][]]+;
    ;fa[x][i];i++)
     fa[x][i+]=fa[fa[x][i]][i];
    ;i<vec[x].size();i++)
     if(!deep[vec[x][i]])
      fa[vec[x][i]][]=x,dfs(vec[x][i]);
}
int lca(int x,int y)
{
    if(deep[x]>deep[y]) swap(x,y);
    ;i>=;i--)
     if(deep[fa[y][i]]>=deep[x])
      y=fa[y][i];
    if(x==y) return x;
    ;i>=;i--)
     if(fa[x][i]!=fa[y][i])
      x=fa[x][i],y=fa[y][i];
    ];
}
int main()
{
    freopen("easy_LCA.in","r",stdin);
    freopen("easy_LCA.out","w",stdout);
    n=read();;
    ;i<=n;i++) a[i]=read();
    ;i<n;i++)
    {
        x=read(),y=read();
        vec[x].push_back(y);
        vec[y].push_back(x);
    }
    deep[]=;
    dfs();
    ;i<=n;i++)
     ;j<=i;j++)
      if(i==j) ans+=a[i];
      else ans+=a[lca(i,j)];
    printf("%lld",ans);
    ;
}

lca T成狗、、、、

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 1000100
using namespace std;
int n,x,y,tot;
long long w[N],fa[N],sum[N],ans,head[N];
int read()
{
    ,f=;char ch=getchar();
    ; ch=getchar();}
    +ch-'; ch=getchar();}
    return x*f;
}
struct Edge
{
    int to,next;
}edge[N<<];
int add(int x,int y)
{
    tot++;
    edge[tot].to=y;
    edge[tot].next=head[x];
    head[x]=tot;
}
int dfs(int x)
{
    sum[x]=;
    for(int i=head[x];i;i=edge[i].next)
    {
        int to=edge[i].to;
        if(to!=fa[x])
        {
            fa[to]=x;dfs(to);
            ans+=(long long)sum[x]*sum[to]*(long long)w[x];
            sum[x]+=(long long)sum[to];
        }
    }
}
int main()
{
    freopen("easy_LCA.in","r",stdin);
    freopen("easy_LCA.out","w",stdout);
    n=read();
    ;i<=n;i++) w[i]=read();
    ;i<n;i++)
    {
        x=read(),y=read();
        add(x,y);add(y,x);
    }
    dfs();
    ;i<=n;i++) ans+=(long long)w[i];
    printf("%lld",ans);
    ;
}