bzoj 1009: [HNOI2008]GT考试 -- KMP+矩阵

1009: [HNOI2008]GT考试

Time Limit: 1 Sec  Memory Limit: 162 MB

Description

　　阿申准备报名参加GT考试，准考证号为N位数X1X2....Xn(0<=Xi<=9),他不希望准考证号上出现不吉利的数字。
他的不吉利数学A1A2...Am(0<=Ai<=9)有M位，不出现是指X1X2...Xn中没有恰好一段等于A1A2...Am. A1和X1可以为
0

Input

　　第一行输入N,M,K.接下来一行输入M位的数。 N<=10^9,M<=20,K<=1000

Output

　　阿申想知道不出现不吉利数字的号码有多少种，输出模K取余的结果.

Sample Input

4 3 100
111

Sample Output

81

HINT

设a[k][j]为k位后面加一个字母转移到j的方案数，于是：

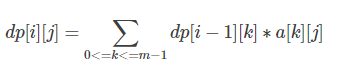
我们发现k后面加一个字母转移到j可以用kmp实现。

这个式子是线性的，可以用矩阵优化。

#include<map>
#include<cmath>
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define inf 1000000007
#define ll long long
#define N 22
#define F(i,r) for(i=0;i<r;i++)
struct zz{int q[N][N];}a,b;
int n,m,p;
zz operator*(zz k,zz l)
{
    int i,j,o;zz z;
    F(i,m) F(j,m) z.q[i][j]=;
    F(i,m) F(j,m) F(o,m)
        z.q[i][j]=(z.q[i][j]+k.q[i][o]*l.q[o][j])%p;
    return z;
}
void ksm(int x)
{
    for(int i=;i<m;i++) b.q[i][i]=;
    while(x)
    {
        if(x&) b=b*a;
        a=a*a;x>>=;
    }
}
char s[N];
int nxt[N],ans;
int main()
{
    scanf("%d%d%d%s",&n,&m,&p,s+);
    for(int i=,j=;i<=m;i++)
    {
        while(j&&s[i]!=s[j+]) j=nxt[j];
        if(s[j+]==s[i]) j++;
        nxt[i]=j;
    }
    for(int i=;i<m;i++)
    {
        for(int j=,x;j<;j++)
        {
            x=i;
            while(x&&s[x+]-''!=j) x=nxt[x];
            if(j==s[x+]-'') a.q[i][x+]++;
            else a.q[i][]++;
        }
    }
    ksm(n);
    for(int i=;i<m;i++) ans+=b.q[][i];
    printf("%d\n",ans%p);
    return ;
}