AC自动机详解（附加可持久化AC自动机）

AC自动机

AC自动机，说白了就是在trie树上跑kmp（其实个人感觉比kmp容易理解）。是一种多匹配串，单个主串的匹配。概括来说，就是将多个匹配串构造一个trie树，对于每个trie树的节点构造nxt指针，最后把主串放在上面跑。

构造trie树

和普通的trie树构建一样，没有什么区别

inline void insert(char *s){
     int l=strlen(s);
     int u=;
     REP(i,,l-){
              int c=calc(s[i]);
              if(!tree[u][c])  tree[u][c]=++total;
              u=tree[u][c];
     }
     isend[u]++;//注意isend的具体处理根据题目而定
     return ;
}

构造nxt数组

其实这一部分是AC自动机的核心，我们这样构造：对于每个节点，它的nxt是，它父亲的nxt的和它名字相同的儿子。如图，u的父亲是v，它父亲的nxt的a这个儿子就是u的nxt。

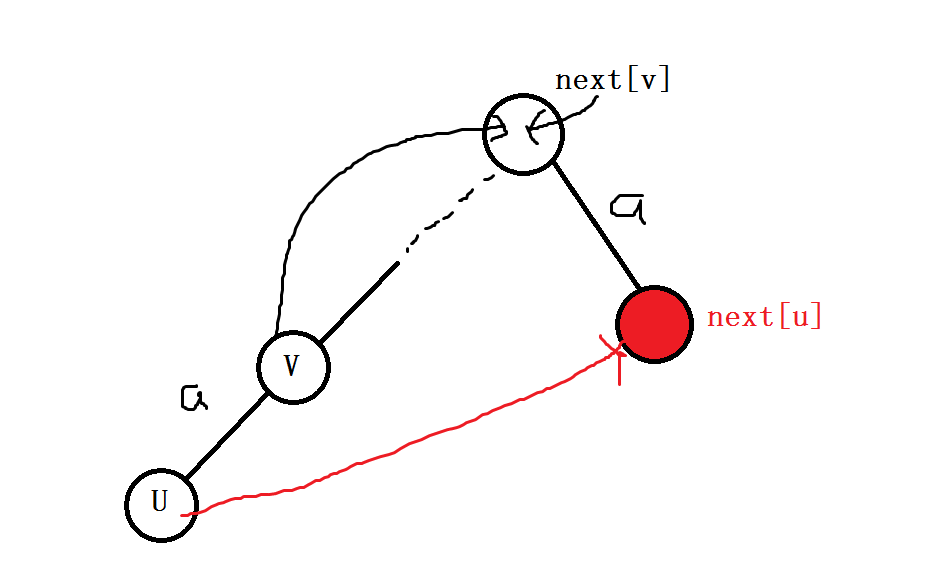
还有一种情况，就是如果节点u，它的没有a这个儿子，那么它就要把nxt[u]的a这个儿子当成他的儿子。

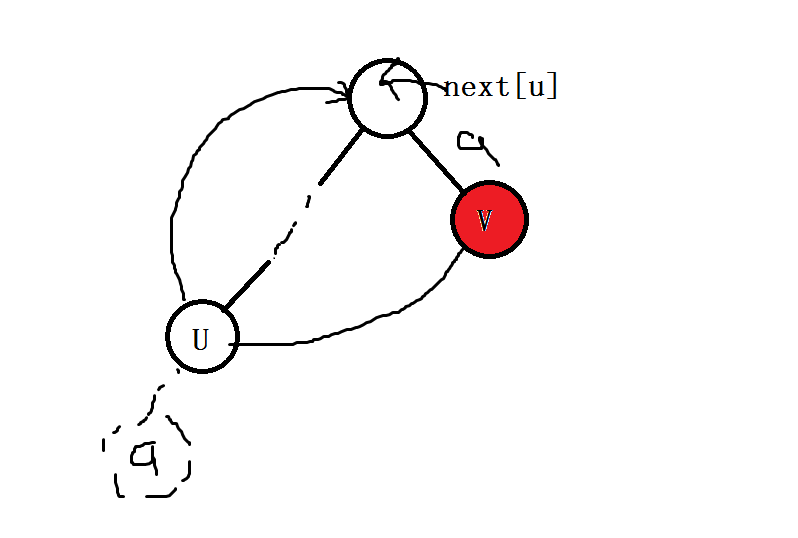
如图，因为u没有a的子节点，所以就连到nxt[u]的a子节点。

那么这么做的原因是什么？我们来看一下这个图：

如图，这个trie树中前7个节点的next都已经构造完成了（箭头表示他们的nxt，1的nxt是0，没有画出来）.现在要找8的next。按照“它的nxt是，它父亲的nxt的和它名字相同的儿子”的原则，我们找到8的父亲，7，发现7的nxt，5也没有B这个儿子，这时候我们需要找5的next，2，最终发现2有B儿子，是4，将8连到4。

但是注意，其实我们这一个一个找nxt是可以省略的。如果按着刚才“因为u没有a的子节点，所以就连到nxt[u]的a子节点。”树就会变成这样（黑线表示连边，红线表示next）

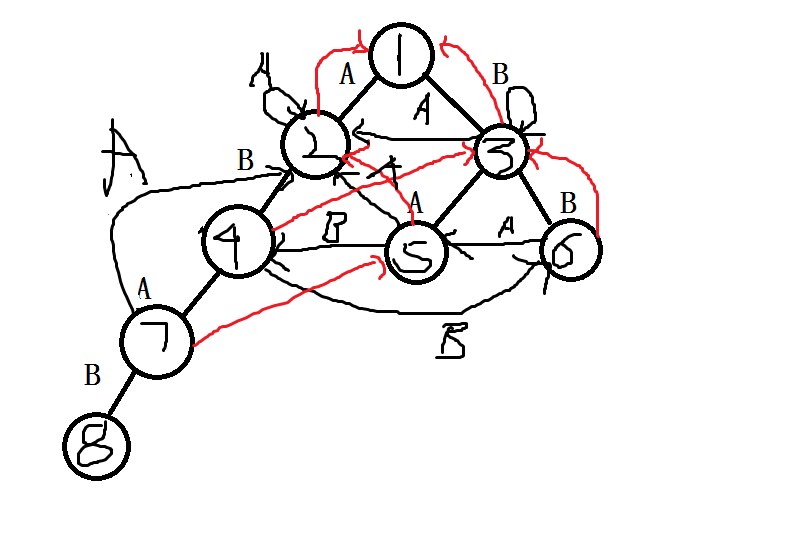
5因为没有B儿子，就把他的nxt：2，的B儿子：4，当成自己的儿子，7也同理，因为它没有A儿子，所以把他的nxt的A儿子：2，当成自己的A儿子。再来看8，发现它的父亲的nxt，5，的B儿子是4，所以自己的next就是4了。这样减少了刚才一个一个找nxt的步骤。

inline void getnxt(){//整个代码用BFS实现
     while(!Q.empty()) Q.pop();
     REP(i,,)  tree[][i]=;//一个非常重要的细节处理，我们加一个虚拟节点0，并将它的所有边都连到1，方便以后的运算
     nxt[]=;
     Q.push();
     while(!Q.empty()){
              int u=Q.front();//u是当前点，这时候nxt[u]已经处理过了，要处理的是u的儿子的nxt，也就是nxt[tree[u][i]]
              Q.pop();
              REP(i,,){//枚举u节点的每一个子节点
                       if(!tree[u][i])  tree[u][i]=tree[nxt[u]][i];//这就是刚才说的很重要的一步优化， 如果自己没有这个子节点，就把自己next的这个子节点当做自己的子节点。
                       else{
                           nxt[tree[u][i]]=tree[nxt[u]][i];//自己儿子的nxt等于自己nxt的儿子，这句话和“自己的nxt是，自己父亲的nxt的和它名字相同的儿子”的意思相同，只是主语从待更新节点变成已就更新节点。
                           Q.push(tree[u][i]);
                       }
              }
    }
    return ;
}

查找

  查找的具体实现是根据题目而定，我就拿这道题举个例子：给一大堆匹配串和一个主串，求有多少个匹配串在主串上出现过。

这种题的做法就是现在构建trie树的时候，把每个单词的结尾都记录一下：isend[i]++。最后跑一遍AC自动机，到每一个节点是ans+=isend[i];isend=0;这样听起来很简单，那么怎么遍历AC自动机呢？

循环遍历主串s，令u表示当前点，每当主串s到下一位时，u=tree[u][s[i]-‘a’]（就是等于它的儿子）。然后对于每个u，循环它的nxt直到根。每到一个点就ans+=isend。具体看代码：

inline void search(){
     int ans=;
     int u=;
     int l=strlen(t);
     REP(i,,l-){//循环遍历主串
              int c=calc(t[i]);//计算这个字符的ACCII码
              int k=tree[u][c];
              while(k>){//对于每一个u遍历它的nxt，直到根
                       if(isend[k]){
                           ans+=isend[k];//加上isend，记录答案
                           isend[k]=;
                       }
                       k=nxt[k];
              }
              u=tree[u][c];//遍历到它的儿子。
     }
     printf("%d\n",ans);

}

总结

再来回顾一下AC自动机的步骤：构建trie树，构建next数组，查找。其中next有两个原则：1、当这个节点没有字符c这个儿子时，把自己的next的c这个儿子当做自己的儿子

2、自己儿子的nxt等于自己nxt的儿子

附上代码：#include <iostream>

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <queue>
#include <stack>
#include <vector>
using namespace std;
#define MAXN 100010
#define INF 10000009
#define MOD 10000007
#define LL long long
#define in(a) a=read()
#define REP(i,k,n) for(int i=k;i<=n;i++)
#define DREP(i,k,n) for(int i=k;i>=n;i--)
#define cl(a) memset(a,0,sizeof(a))
inline int read(){
         int x=,f=;char ch=getchar();
         for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-;
    for(;isdigit(ch);ch=getchar()) x=x*+ch-'';
    return x*f;
}
inline void out(int x){
         if(x<) putchar('-'),x=-x;
         if(x>) out(x/);
         putchar(x%+'');
}
int T,n;
int total=;
int nxt[],tree[][];
char in[];
int isend[];
char t[];
queue <int> Q;
int calc(char c){
         return c-'a';
}
inline void insert(char *s){
         int l=strlen(s);
         int u=;
         REP(i,,l-){
                   int c=calc(s[i]);
                   if(!tree[u][c])  tree[u][c]=++total;
                   u=tree[u][c];
         }
         isend[u]++;
         return ;
}
inline void getnxt(){//整个代码用BFS实现
         while(!Q.empty()) Q.pop();
         REP(i,,)  tree[][i]=;//一个非常重要的细节处理，我们加一个虚拟节点0，并将它的所有边都连到1，方便以后的运算
         nxt[]=;
         Q.push();
         while(!Q.empty()){
                   int u=Q.front();//u是当前点，这时候nxt[u]已经处理过了，要处理的是u的儿子的nxt，也就是nxt[tree[u][i]]
                   Q.pop();
                   REP(i,,){//枚举u节点的每一个子节点
                            if(!tree[u][i])  tree[u][i]=tree[nxt[u]][i];//这就是刚才说的很重要的一步优化， 如果自己没有这个子节点，就把自己next的这个子节点当做自己的子节点。
                            else{
                                nxt[tree[u][i]]=tree[nxt[u]][i];//自己儿子的nxt等于自己nxt的儿子，这句话和“自己的nxt是，自己父亲的nxt的和它名字相同的儿子”的意思相同，只是主语从待更新节点变成已就更新节点。
                                Q.push(tree[u][i]);
                            }
                   }
    }
    return ;
}
inline void search(){
         int ans=;
         int u=;
         int l=strlen(t);
         REP(i,,l-){//循环遍历主串
                   int c=calc(t[i]);//计算这个字符的ACCII码
                   int k=tree[u][c];
                   while(k>){//对于每一个u遍历它的nxt，直到根
                            if(isend[k]){
                                ans+=isend[k];//加上isend，记录答案
                                isend[k]=;
                            }
                            k=nxt[k];
                   }
                   u=tree[u][c];//遍历到它的儿子。
         }
         printf("%d\n",ans);
}
int main(){
         in(T);
         while(T--){
                   total=;
                   cl(nxt);
                   cl(tree);
                   cl(isend);
                   in(n);
                   REP(i,,n){
                            scanf("%s",in);
                            insert(in);
                   }
                   scanf("%s",t);
                   getnxt();
                   search();
         }
    return ;
}
 

附加：可持久化AC自动机

如果你希望每当你查找到一个字符串，然后要把它删去时，就需要可持久化AC自动机。其实和普通的AC自动机很像，唯一区别是查找的时候去掉了对于每一个u遍历nxt直到根的步骤，然后让每个u都压进栈，遇到end就弹出栈里面此字符串长度的元素。