Codeforces Round #323 (Div. 2) C. GCD Table map

题目链接：http://codeforces.com/contest/583/problem/C

C. GCD Table

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

The GCD table G of size n × n for an array of positive integers a of length n is defined by formula

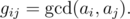
Let us remind you that the greatest common divisor (GCD) of two positive integers x and y is the greatest integer that is divisor of both xand y, it is denoted as 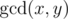. For example, for array a = {4, 3, 6, 2} of length 4 the GCD table will look as follows:

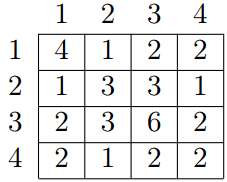
Given all the numbers of the GCD table G, restore array a.

Input

The first line contains number n (1 ≤ n ≤ 500) — the length of array a. The second line contains n2 space-separated numbers — the elements of the GCD table of G for array a.

All the numbers in the table are positive integers, not exceeding 109. Note that the elements are given in an arbitrary order. It is guaranteed that the set of the input data corresponds to some array a.

Output

In the single line print n positive integers — the elements of array a. If there are multiple possible solutions, you are allowed to print any of them.

Examples

input

4
2 1 2 3 4 3 2 6 1 1 2 2 1 2 3 2

output

4 3 6 2

input

1
42

output

42 

input

2
1 1 1 1

output

1 1 

题意：你有n个数，给你n个数相互的gcd，即 gcd(a[i],a[j]) 1<=i<=n ,1<=j<=n;

　　　 让你求原来n个数 a[i]，随意输出；

思路：首先，发现对称，好像没有什么用；

　　　显然gcd只可能变小对吧，所以我们取最大的那个是必然存在的，放入a组数中，然后继续找下一个；

　　　记得删掉取得数，和取数之间的gcd即可；

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define mk make_pair
#define eps 1e-7
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=1e4+,M=4e6+,inf=;
const ll INF=1e18+,mod=;

///   数组大小
map<int,int>mp;
map<int,int>::iterator it;
vector<int>ans;
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=;i<=n*n;i++)
    {
        int x;
        scanf("%d",&x);
        mp[x]++;
    }
    for(int i=;i<=n;i++)
    {
        it=--mp.end();
        int z=it->first;
        for(int j=;j<ans.size();j++)
        {
            int g=__gcd(z,ans[j]);
            mp[g]--;
            mp[g]--;
            if(!mp[g])mp.erase(mp.find(g));
        }
        ans.push_back(z);
        mp[z]--;
        if(!mp[z])mp.erase(mp.find(z));
    }
    for(int i=;i<n;i++)
        cout<<ans[i]<<" ";
    return ;
}